There is a variation of the 75-Number Bingo game that randomly picks numbers from a set of 90 numbers. In this variation a “Bingo” consists of filling 1, 2, or 3 rows. A typical Bingo board for this 90 number game has 3 rows and 9 columns and could look like the following:


   The 12 stars are free spaces while there are 15 random numbers ranging from 1 to 90. (Some versions of the game have blanks instead of stars. Also, for the calculations given here, each row must have 5 numbers and 4 stars.) The stars and numbers may be arranged randomly across each row. As numbers are called, a marker is used to cover a space if the called number matches one of the numbers on your board. If you completely fill any row with a combination of markers and free spaces (or multiple rows depending on the “win” definition), you have a Bingo.


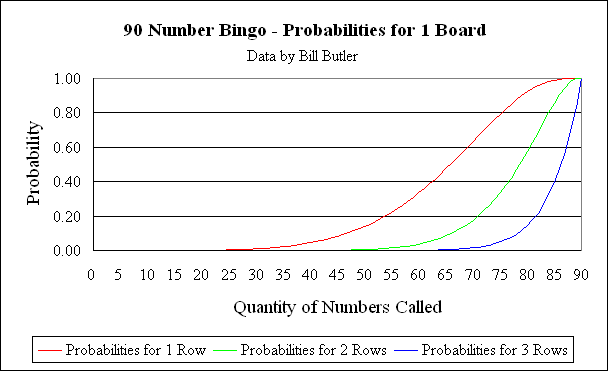
   The red line in the above graph shows the probability that a single board will score a 1-row Bingo on or before the “Nth” number is called. The green line shows the probability that a single board will score a 2-row Bingo on or before the “Nth” number is called. Finally the blue line shows similar data to fill all three rows (fill all spaces) for a single board. Exact statistical numbers are given in the table below.


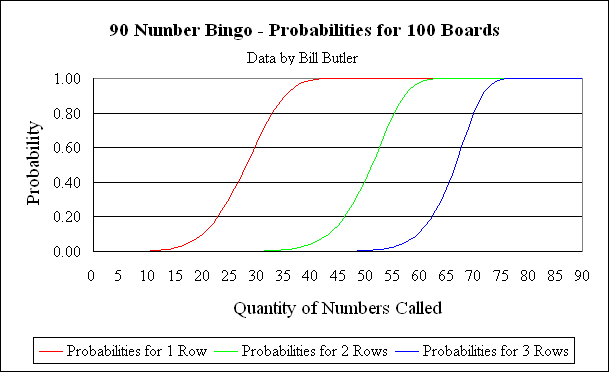
   The above graph shows probabilities if there are 100 boards in play for a 90-number game. (Calculations assume that all boards are randomly independent.) The red line shows the probability that at least one board will fill a row on or before the “Nth” number is called. The green line shows the probability that at least one board will fill 2 rows on or before the “Nth” number is called. Finally, the blue line shows the probability that at least one board will fill all three rows on or before the “Nth” number is called.


   The table below gives the statistics for the above graphs. The first column shows how many numbers have been called. The second column shows the probability that a single board will fill one row on or before a given quantity of numbers have been called. The third column shows the probability that at least 1 board out of 100 will fill a row on or before a given quantity of numbers have been called. Columns 4 - 7 show similar paired probabilities for 2 and 3 row fills.

   For example, by the time 50 numbers have been called, there is a 0.139290 probability that a single board will have filled 1 row. If 100 boards are in play, then there is a 0.411553 probability that at least 1 of these boards has filled 2 rows.

Quantity  Cumulative  Cumulative  Cumulative  Cumulative  Cumulative  Cumulative
of Bingo  Prob. of    Prob. of    Prob. of    Prob. of    Prob. of    Prob. of
Numbers   1 row fill  1 row fill  2 row fill  2 row fill  3 row fill  3 row fill
Picked    1 Board     100 Boards  1 Board     100 Boards  1 Board     100 Boards
--------------------------------------------------------------------------------
   5      0.000000    0.000007
   6      0.000000    0.000041
   7      0.000001    0.000143
   8      0.000004    0.000382
   9      0.000009    0.000860
  10      0.000017    0.001719    0.000000    0.000000
  11      0.000032    0.003149    0.000000    0.000000
  12      0.000054    0.005392    0.000000    0.000000
  13      0.000088    0.008747    0.000000    0.000000
  14      0.000137    0.013574    0.000000    0.000000
  15      0.000205    0.020292    0.000000    0.000000    0.000000    0.000000
  16      0.000298    0.029380    0.000000    0.000000    0.000000    0.000000
  17      0.000422    0.041368    0.000000    0.000001    0.000000    0.000000
  18      0.000585    0.056822    0.000000    0.000002    0.000000    0.000000
  19      0.000794    0.076330    0.000000    0.000005    0.000000    0.000000
  20      0.001058    0.100465    0.000000    0.000010    0.000000    0.000000
  21      0.001389    0.129756    0.000000    0.000018    0.000000    0.000000
  22      0.001797    0.164634    0.000000    0.000034    0.000000    0.000000
  23      0.002296    0.205382    0.000001    0.000060    0.000000    0.000000
  24      0.002900    0.252075    0.000001    0.000103    0.000000    0.000000
  25      0.003625    0.304522    0.000002    0.000171    0.000000    0.000000
  26      0.004487    0.362212    0.000003    0.000278    0.000000    0.000000
  27      0.005506    0.424287    0.000004    0.000442    0.000000    0.000000
  28      0.006702    0.489534    0.000007    0.000688    0.000000    0.000000
  29      0.008096    0.556418    0.000011    0.001050    0.000000    0.000000
  30      0.009712    0.623156    0.000016    0.001574    0.000000    0.000000
  31      0.011575    0.687842    0.000023    0.002322    0.000000    0.000001
  32      0.013712    0.748600    0.000034    0.003375    0.000000    0.000001
  33      0.016152    0.803757    0.000048    0.004838    0.000000    0.000002
  34      0.018925    0.852017    0.000069    0.006845    0.000000    0.000004
  35      0.022063    0.892583    0.000096    0.009567    0.000000    0.000007
  36      0.025600    0.925234    0.000133    0.013218    0.000000    0.000012
  37      0.029572    0.950303    0.000182    0.018063    0.000000    0.000020
  38      0.034015    0.968593    0.000247    0.024423    0.000000    0.000034
  39      0.038969    0.981217    0.000332    0.032689    0.000001    0.000055
  40      0.044472    0.989424    0.000443    0.043320    0.000001    0.000088
  41      0.050568    0.994423    0.000585    0.056852    0.000001    0.000139
  42      0.057298    0.997262    0.000767    0.073891    0.000002    0.000215
  43      0.064705    0.998756    0.000999    0.095105    0.000003    0.000331
  44      0.072835    0.999480    0.001291    0.121202    0.000005    0.000502
  45      0.081732    0.999802    0.001658    0.152895    0.000008    0.000753
  46      0.091442    0.999932    0.002115    0.190841    0.000011    0.001117
  47      0.102008    0.999979    0.002683    0.235570    0.000016    0.001640
  48      0.113477    0.999994    0.003382    0.287378    0.000024    0.002384
  49      0.125890    0.999999    0.004241    0.346215    0.000034    0.003435
  50      0.139290    1.000000    0.005289    0.411553    0.000049    0.004903
  51      0.153717    1.000000    0.006562    0.482280    0.000070    0.006939
  52      0.169208    1.000000    0.008101    0.556632    0.000098    0.009738
  53      0.185797    1.000000    0.009953    0.632214    0.000136    0.013557
  54      0.203514    1.000000    0.012172    0.706136    0.000189    0.018722
  55      0.222383    1.000000    0.014819    0.775295    0.000260    0.025653
  56      0.242425    1.000000    0.017963    0.836777    0.000355    0.034874
  57      0.263650    1.000000    0.021683    0.888319    0.000482    0.047036
  58      0.286064    1.000000    0.026064    0.928711    0.000650    0.062923
  59      0.309661    1.000000    0.031206    0.958010    0.000871    0.083464
  60      0.334429    1.000000    0.037215    0.977461    0.001162    0.109723
  61      0.360342    1.000000    0.044210    0.989129    0.001540    0.142857
  62      0.387361    1.000000    0.052321    0.995364    0.002032    0.184046
  63      0.415436    1.000000    0.061690    0.998283    0.002667    0.234361
  64      0.444501    1.000000    0.072468    0.999459    0.003483    0.294562
  65      0.474475    1.000000    0.084821    0.999859    0.004528    0.364825
  66      0.505258    1.000000    0.098921    0.999970    0.005860    0.444415
  67      0.536734    1.000000    0.114951    0.999995    0.007551    0.531358
  68      0.568769    1.000000    0.133100    0.999999    0.009687    0.622229
  69      0.601207    1.000000    0.153562    1.000000    0.012378    0.712222
  70      0.633874    1.000000    0.176530    1.000000    0.015754    0.795661
  71      0.666577    1.000000    0.202194    1.000000    0.019974    0.867032
  72      0.699102    1.000000    0.230737    1.000000    0.025231    0.922342
  73      0.731219    1.000000    0.262321    1.000000    0.031756    0.960327
  74      0.762678    1.000000    0.297086    1.000000    0.039829    0.982827
  75      0.793217    1.000000    0.335132    1.000000    0.049787    0.993945
  76      0.822562    1.000000    0.376511    1.000000    0.062029    0.998344
  77      0.850434    1.000000    0.421209    1.000000    0.077036    0.999670
  78      0.876551    1.000000    0.469125    1.000000    0.095378    0.999956
  79      0.900639    1.000000    0.520051    1.000000    0.117733    0.999996
  80      0.922438    1.000000    0.573644    1.000000    0.144902    1.000000
  81      0.941718    1.000000    0.629392    1.000000    0.177834    1.000000
  82      0.958285    1.000000    0.686579    1.000000    0.217647    1.000000
  83      0.972006    1.000000    0.744239    1.000000    0.265658    1.000000
  84      0.982822    1.000000    0.801108    1.000000    0.323410    1.000000
  85      0.990776    1.000000    0.855561    1.000000    0.392712    1.000000
  86      0.996037    1.000000    0.905545    1.000000    0.475679    1.000000
  87      0.998936    1.000000    0.948502    1.000000    0.574779    1.000000
  88      1.000000    1.000000    0.981273    1.000000    0.692884    1.000000
  89      1.000000    1.000000    1.000000    1.000000    0.833333    1.000000
  90      1.000000    1.000000    1.000000    1.000000    1.000000    1.000000




   The free spaces on the board do not play a part in the probability calculations. Thus calculations use a 3 row by 5 column board.

   The probability of any “1-Board” entry in the above table is the sum of the probabilities of all the various ways that the event in question can happen. As an example, we will show how to calculate the probability that a single board can fill at least one row by the time 40 numbers have been called.

   The probability that a single board has filled at least one row by the time 40 numbers have been called is equal to the sum of:

The probability that exactly 5 of the 40 called numbers are on the board times the probability that these 5 numbers complete a row.
Plus
The probability that exactly 6 of the 40 called numbers are on the board times the probability that these 6 numbers complete a row.
Plus
The probability that exactly 7 of the 40 called numbers are on the board times the probability that these 7 numbers complete a row.
Etc.
The probability that exactly 15 of the 40 called numbers are on the board times the probability that these 15 numbers complete a row.

The first part of any of the, “exactly N of the 40 called numbers…” is:

Prob. = COMBIN(15, N) * COMBIN(90-15, 40-N) / COMBIN(90, 40)
If we are calculating for 6 on the board this becomes:
Prob. = COMBIN(15, 6) * COMBIN(75, 34) / COMBIN(90, 40) = 0.209994

   For the second half of this calculation we have to calculate the following table which shows how many times a bingo exists given that “N” hits are randomly placed on the board.

Number   Number     Number of     Number of     Number of
 Hits    Combin.   1-row fills   2-row fills   3-row fills
   0          1           0             0             0
   1         15           0             0             0
   2        105           0             0             0
   3        455           0             0             0
   4      1,365           0             0             0
   5      3,003           3             0             0
   6      5,005          30             0             0
   7      6,435         135             0             0
   8      6,435         360             0             0
   9      5,005         630             0             0
  10      3,003         753             3             0
  11      1,365         615            15             0
  12        455         330            30             0
  13        105         105            30             0
  14         15          15            15             0
  15          1           1             1             1

   The table itself can be calculated by either some convoluted combinatorics or as part of a computer program that generates all combinations and counts the results. If we look at row 6 we see that there are 5005 possible ways that you can hit 6 of the 15 numbers on the Bingo board. 30 of these combinations will produce a 1 row fill. Thus if you randomly mark 6 of the 15 numbers on the board, there will be a 30 / 5005 = 0.005994 chance that you will have a 1 row Bingo.

   Finally, we multiply our two partial results together to find that if 40 numbers have been called in a game, and if exactly 6 of these hit on your Bingo card, then there is a 0.209994 * 0.005994 = 0.0012587 probability that this particular combination will result in a Bingo.

   Next, repeat all the above calculations for 5, 7, 8, 9, 10, 11, 12, 13, 14, and 15 hits on the board. Add all of these partial amounts together. The result will be the 0.044472 value shown in the table as the probability that a single board will have a Bingo by the time 40 numbers have been called.

   Next, call in your handy dandy computer program for all these calculations.

   The 100-board probabilities are easy once you have the single board result. For example, the probability that at least 1 of the 100 boards will have a 1 row bingo after 40 calls is: 1-(1-0.044472)^100  = 0.989424.


Return to the main Bingo page


Web page generated via Sea Monkey's Composer
within  a Linux Cinnamon Mint 18 operating system.
(Goodbye Microsoft)