Suppose you are organizing a Bridge round robin tournament (Could also be tennis doubles, partnership golf, partnership horseshoes, etc.), and to equally mix the partnership/opponent pairs, you would like to have every player have every other player as a partner once and as an opponent twice. For example, if there are 8 players “A”, “B”, “C”, “D”, “E”, “F”, “G”, and “H”, you will have two tables of Bridge players. Suppose you wish to arrange a sequential seating arrangement such that after 7 rounds of Bridge:

Player “A” has had player “B” as a partner once and as an opponent twice.
Player “A” has had player “C” as a partner once and as an opponent twice.
Player “A” has had player “D” as a partner once and as an opponent twice.
Player “A” has had player “E” as a partner once and as an opponent twice.
Player “A” has had player “F” as a partner once and as an opponent twice.
Player “A” has had player “G” as a partner once and as an opponent twice.
Player “A” has had player “H” as a partner once and as an opponent twice.

Player “B” has had player “A” as a partner once and as an opponent twice.
Player “B” has had player “C” as a partner once and as an opponent twice.
Player “B” has had player “D” as a partner once and as an opponent twice.
Player “B” has had player “E” as a partner once and as an opponent twice.
etc.
for all possible combinations.


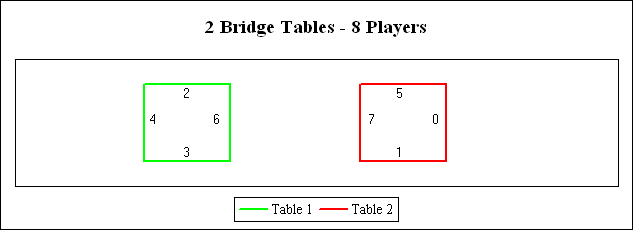
   The diagram above shows one of the 6 intrinsically different position solutions for a 2-table round-robin tournament. (There are multiple permutations within these 6 patterns.) To solve the problem, start with player “A” at position “0”, player “B” at position “1”, player “C” at position “2”, etc. for the first round of play. When the first round of play is over, player “A” stays at position “0”, and all other players advance to the next higher “position”. (With the exception of the person who was at “7” who instead cycles back to position “1”.) This same advancement/cycle sequence is repeated for the third round, etc. The full sequence of who sits where for each round then becomes:

Round   Player  Player  Player  Player  Player  Player  Player  Player
 Nbr.     A       B       C       D       E       F       G       H
  1       0       1       2       3       4       5       6       7
  2       0       2       3       4       5       6       7       1
  3       0       3       4       5       6       7       1       2
  4       0       4       5       6       7       1       2       3
  5       0       5       6       7       1       2       3       4
  6       0       6       7       1       2       3       4       5
  7       0       7       1       2       3       4       5       6

   Each entry in the above table shows the Bridge table position/location that each person should go to on each of the 7 rounds of the tournament. When all 7 rounds have finished, each player will have had each other player as a partner once and as an opponent twice.

A shorthand summary for this particular 2-table solution plus the other 5 solutions is thus:

Solution    <---- Table 1 ---->     <---- Table 2 ---->
   1        2 and 3 vs. 4 and 6     5 and 1 vs. 7 and 0
   2        2 and 3 vs. 5 and 1     4 and 6 vs. 7 and 0
   3        2 and 3 vs. 7 and 0     4 and 6 vs. 5 and 1
   4        4 and 5 vs. 1 and 3     6 and 2 vs. 7 and 0
   5        4 and 5 vs. 6 and 2     1 and 3 vs. 7 and 0
   6        4 and 5 vs. 7 and 0     1 and 3 vs. 6 and 2




A Solution for 3 Bridge Tables (12 players)

   The diagram below shows one of the table position definitions that will solve the problem for 12 players. (There are 20 intrinsically different cyclical solutions - each of which has a large number of permutations.)


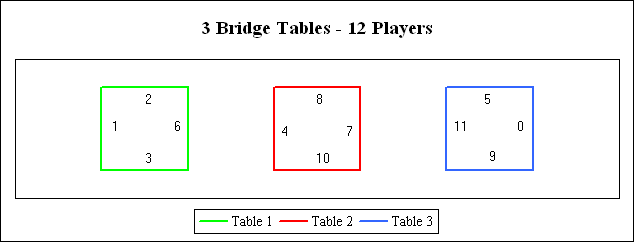
Solution  <----- Table 1 ----->   <----- Table 2 ----->   <----- Table 3 ----->
   1      2 and 3  vs.  1 and 6   8 and 10 vs.  4 and 7   5 and 9  vs. 11 and 0

The complete cycle sequence for these 12 players would be:

Round  Plr Plr Plr Plr   Plr Plr Plr Plr   Plr Plr Plr Plr
 Nbr    A   B   C   D     E   F   G   H     I   J   K   L
  1     2   3   1   6     8  10   4   7     5   9  11   0
  2     3   4   2   7     9  11   5   8     6  10   1   0
  3     4   5   3   8    10   1   6   9     7  11   2   0
  4     5   6   4   9    11   2   7  10     8   1   3   0
  5     6   7   5  10     1   3   8  11     9   2   4   0
  6     7   8   6  11     2   4   9   1    10   3   5   0
  7     8   9   7   1     3   5  10   2    11   4   6   0
  8     9  10   8   2     4   6  11   3     1   5   7   0
  9    10  11   9   3     5   7   1   4     2   6   8   0
 10    11   1  10   4     6   8   2   5     3   7   9   0
 11     1   2  11   5     7   9   3   6     4   8  10   0

Again, when all 11 rounds have finished, each player will have had each other player as a partner once and as an opponent twice.

   There is considerable latitude in setting up a system that will work. While the above examples list the players in alphabetical order, this is not necessary. Players can start at any random position. Also the table numbers can be permuted in any order. For 3 tables the names “Table 1”, “Table 2”, and “Table 3” can be permuted in any of 3 x 2 x 1 = 6 ways. Also, the north-south and east-west definitions can be swapped and the compass directions of the tables can be rotated. Finally, there are solutions using a complementary numbering system which has the effect of reversing the cycle sequence. However, for any individual table, the numeric pairs must be matched as above. (E.g. for Table 1 in the above example, Positions 2 and 3 must be opposite each other, and the other 2 positions must be 1 and 6.)

The other 19 solutions are:

Solution  <----- Table 1 ----->   <----- Table 2 ----->   <----- Table 3 ----->
   2       9 & 10  vs.   5 &  7    1 &  4  vs.  11 &  0    2 &  6  vs.   3 &  8
   3       1 &  2  vs.   4 &  6    7 & 10  vs.  11 &  0    5 &  9  vs.   3 &  8
   4       8 &  9  vs.   5 & 10    1 &  3  vs.   4 &  7    2 &  6  vs.  11 &  0
   5       4 &  5  vs.   9 &  2    8 & 10  vs.  11 &  0    3 &  6  vs.   7 &  1
   6       8 &  9  vs.   4 &  6    2 &  5  vs.  10 &  3    7 &  1  vs.  11 &  0
   7       8 &  9  vs.   4 &  6    2 &  5  vs.   7 &  1   10 &  3  vs.  11 &  0
   8       8 &  9  vs.   7 &  1    4 &  6  vs.  10 &  3    2 &  5  vs.  11 &  0
   9       8 &  9  vs.   7 &  1    4 &  6  vs.  11 &  0    2 &  5  vs.  10 &  3
  10       8 &  9  vs.  11 &  0    4 &  6  vs.  10 &  3    2 &  5  vs.   7 &  1
  11       4 &  5  vs.  11 &  0   10 &  1  vs.   8 &  2    6 &  9  vs.   3 &  7
  12       5 &  6  vs.   1 &  4    7 &  9  vs.  10 &  3    8 &  2  vs.  11 &  0
  13       6 &  7  vs.  11 &  0   10 &  1  vs.   9 &  3    2 &  5  vs.   4 &  8
  14       5 &  6  vs.   7 & 10    2 &  4  vs.   8 &  1    9 &  3  vs.  11 &  0
  15       2 &  3  vs.   5 &  7    6 &  9  vs.   8 &  1   10 &  4  vs.  11 &  0
  16       2 &  3  vs.   5 &  7    6 &  9  vs.  10 &  4    8 &  1  vs.  11 &  0
  17       2 &  3  vs.  10 &  4    5 &  7  vs.   8 &  1    6 &  9  vs.  11 &  0
  18       2 &  3  vs.  10 &  4    5 &  7  vs.  11 &  0    6 &  9  vs.   8 &  1
  19       2 &  3  vs.  11 &  0    5 &  7  vs.   8 &  1    6 &  9  vs.  10 &  4
  20       6 &  7  vs.   9 &  2    1 &  3  vs.  11 &  0    5 &  8  vs.  10 &  4



Other Table Configurations

   There are cyclic solutions for larger numbers of tables. (Number of players always equals 4 times the number of tables.) If there is only 1 table (4 players), the answer is trivial. One player remains at position “0” and the other 3 players sequence in either a clockwise or counterclockwise direction.


A solution for 4 Bridge Tables (16 players) (Selected from a total of 128 solutions)

   Rapidly increasing numbers of solutions exist for all larger numbers of Bridge tables. The solution below defines a table-position numbering system that will allow each player to have each other player as a partner once and as an opponent twice. Players can be seated randomly, and thereafter sequence/cycle as in the earlier examples.

Table 1    12 and 13  vs.   3 and  9
Table 2     4 and  6  vs.  14 and  2
Table 3     7 and 11  vs.   5 and 10
Table 4     1 and  8  vs.  15 and  0

The starting positions for all 128 cyclical Bridge/Whist Tournament Schedules for 16 players can be seen here.
http://www.durangobill.com/BridgePics/bridge16data.txt



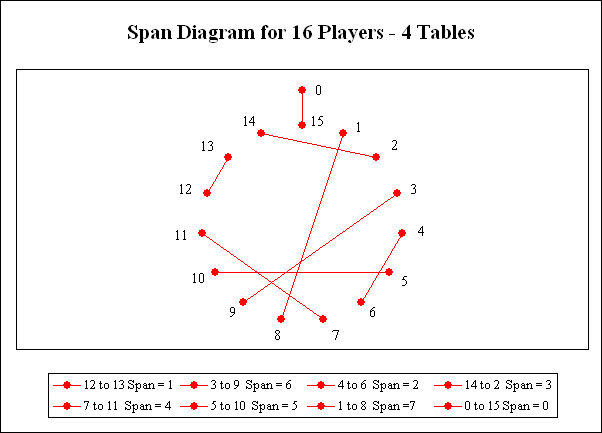
   The diagram above shows how the partnerships for the above solution are calculated. To find a solution for the round robin problem, the first step is to match the positions into teams. Place the numbers 1 to 15 around the circumference of a circle, and then connect pairs so that the span distances (chord distances) are all different. See the “Combinatorics and the Computer Algorithm” section below for additional information.



A solution for 5 Bridge Tables (20 players) (Selected from a total of 1,710 solutions)

Table 1    14 and 15  vs.  19 and  0
Table 2    16 and 18  vs.   1 and 10
Table 3     4 and  7  vs.   6 and 13
Table 4     5 and  9  vs.  12 and 17
Table 5     2 and  8  vs.   3 and 11

The starting positions for all 1,710 cyclical Bridge/Whist Tournament Schedules for 20 players can be seen here.
http://www.durangobill.com/BridgePics/bridge20data.txt


A solution for 6 Bridge Tables (24 players) (Selected from a total of 81,576 solutions)

Table 1    17 and 18  vs.   3 and 13
Table 2    20 and 22  vs.   6 and  9
Table 3    15 and 19  vs.   8 and 16
Table 4     5 and 10  vs.   2 and 11
Table 5    21 and  4  vs.  23 and  0
Table 6     7 and 14  vs.   1 and 12

The starting positions for the first 1,000 cyclical Bridge/Whist Tournament Schedules for 24 players can be seen here.
http://www.durangobill.com/BridgePics/bridge24data.txt


A solution for 7 Bridge Tables (28 players) (Selected from a total of 7,910,127 solutions)

Table 1    22 and 23  vs.   1 and 14
Table 2     5 and  7  vs.   8 and 17
Table 3     9 and 12  vs.   4 and 11
Table 4    21 and 25  vs.  10 and 18
Table 5    19 and 24  vs.   3 and 15
Table 6    20 and 26  vs.   6 and 16
Table 7     2 and 13  vs.  27 and  0

   Most of the solutions for 28 players have a mirror image. (See the 13-player section near the end of the page for more on mirror images.) However there are 27 solutions that are their own mirror image – which is why the total number of solutions for 28 players is an odd number. Here is an example of a solution which is its own mirror image.

Table 1    13 and 14  vs.  26 and  1
Table 2    12 and 15  vs.  10 and 17
Table 3    25 and  2  vs.   9 and 18
Table 4    11 and 16  vs.   8 and 19
Table 5    24 and  3  vs.   7 and 20
Table 6    23 and  4  vs.  22 and  5
Table 7    21 and  6  vs.  27 and  0

Note that the sum of the positions for each team is 27. Also, the “Span Diagram” for any of these “special” solutions, will have parallel horizontal lines for the chords connecting player positions to form teams.

The starting positions for the first 1,000 cyclical Bridge/Whist Tournament Schedules for 28 players can be seen here.
http://www.durangobill.com/BridgePics/bridge28data.txt


A solution for 8 Bridge Tables (32 players) (Selected from 1,028,654,070 solutions)

Table 1    24 and 25  vs.  31 and  0
Table 2     9 and 11  vs.  28 and  5
Table 3    10 and 13  vs.  22 and 26
Table 4     7 and 12  vs.   2 and 15
Table 5    21 and 27  vs.  20 and 29
Table 6    23 and 30  vs.   8 and 19
Table 7     4 and 14  vs.   3 and 17
Table 8     6 and 18  vs.   1 and 16

The starting positions for the first 1,000 cyclical Bridge/Whist Tournament Schedules for 32 players can be seen here.
http://www.durangobill.com/BridgePics/bridge32data.txt


A solution for 9 Bridge Tables (36 players)

Table 1    26 and 27  vs.  11 and 22
Table 2    29 and 31  vs.   3 and 19
Table 3     9 and 12  vs.   6 and 20
Table 4    10 and 14  vs.  23 and 30
Table 5    28 and 33  vs.   4 and 16
Table 6     7 and 13  vs.   8 and 21
Table 7    24 and 32  vs.  25 and 34
Table 8     5 and 15  vs.   1 and 18
Table 9     2 and 17  vs.  35 and  0

The starting positions for the first 1,000 cyclical Bridge/Whist Tournament Schedules for 36 players can be seen here.
http://www.durangobill.com/BridgePics/bridge36data.txt


A solution for 10 Bridge Tables (40 players)

Table 1    33 and 34  vs.   5 and 17
Table 2    29 and 31  vs.  11 and 24
Table 3    12 and 15  vs.  26 and 36
Table 4     9 and 13  vs.   6 and 22
Table 5    27 and 32  vs.  28 and 35
Table 6    10 and 16  vs.   4 and 18
Table 7    30 and 38  vs.   3 and 21
Table 8    37 and  7  vs.   8 and 23
Table 9    14 and 25  vs.   1 and 20
Table 10    2 and 19  vs.  39 and  0

The starting positions for the first 1,000 cyclical Bridge/Whist Tournament Schedules for 40 players can be seen here.
http://www.durangobill.com/BridgePics/bridge40data.txt


A solution for 11 Bridge Tables (44 players)

Table 1     9 and 10  vs.   5 and 19
Table 2    33 and 35  vs.   4 and 20
Table 3    12 and 15  vs.   1 and 22
Table 4    13 and 17  vs.  30 and 38
Table 5    32 and 37  vs.  11 and 26
Table 6    36 and 42  vs.  34 and 41
Table 7    31 and 40  vs.  16 and 28
Table 8    29 and 39  vs.   2 and 21
Table 9     7 and 18  vs.  14 and 27
Table 10    8 and 25  vs.   6 and 24
Table 11    3 and 23  vs.  43 and  0

The starting positions for the first 1,000 cyclical Bridge/Whist Tournament Schedules for 44 players can be seen here.
http://www.durangobill.com/BridgePics/bridge44data.txt


A solution for 12 Bridge Tables (48 players)

Table 1    35 and 36  vs.  19 and 31
Table 2    37 and 39  vs.   4 and 22
Table 3    12 and 15  vs.   5 and 21
Table 4    13 and 17  vs.   2 and 23
Table 5    40 and 45  vs.  32 and 43
Table 6    38 and 44  vs.  10 and 18
Table 7    34 and 41  vs.  16 and 30
Table 8    33 and 42  vs.  11 and 28
Table 9    46 and  9  vs.   8 and 27
Table 10    7 and 20  vs.  47 and  0
Table 11   14 and 29  vs.   6 and 26
Table 12    3 and 25  vs.   1 and 24

The starting positions for the first 1,000 cyclical Bridge/Whist Tournament Schedules for 48 players can be seen here.
http://www.durangobill.com/BridgePics/bridge48data.txt


A solution for 13 Bridge Tables (52 players)

Table 1    41 and 42  vs.  39 and 48
Table 2    38 and 40  vs.  12 and 15
Table 3    13 and 17  vs.   2 and 25
Table 4    45 and 50  vs.  36 and 46
Table 5    43 and 49  vs.  14 and 31
Table 6    37 and 44  vs.   4 and 24
Table 7    10 and 18  vs.   1 and 26
Table 8     9 and 20  vs.  19 and 33
Table 9    35 and 47  vs.   6 and 28
Table 10   21 and 34  vs.  51 and  0
Table 11    7 and 22  vs.   3 and 27
Table 12   16 and 32  vs.  11 and 30
Table 13    5 and 23  vs.   8 and 29

The starting positions for the first 1,000 cyclical Bridge/Whist Tournament Schedules for 52 players can be seen here.
http://www.durangobill.com/BridgePics/bridge52data.txt


A solution for 14 Bridge Tables (56 players)

Table 1    44 and 45  vs.   5 and 25
Table 2    41 and 43  vs.  15 and 18
Table 3    13 and 17  vs.   3 and 29
Table 4    48 and 53  vs.  40 and 47
Table 5    46 and 52  vs.   1 and 28
Table 6    12 and 20  vs.  38 and 50
Table 7    42 and 51  vs.  55 and  0
Table 8    39 and 49  vs.   6 and 30
Table 9    54 and 10  vs.   8 and 31
Table 10    9 and 22  vs.  14 and 33
Table 11   23 and 37  vs.  16 and 34
Table 12   21 and 36  vs.  19 and 35
Table 13    7 and 24  vs.   2 and 27
Table 14   11 and 32  vs.   4 and 26

The starting positions for the first 1,000 cyclical Bridge/Whist Tournament Schedules for 56 players can be seen here.
http://www.durangobill.com/BridgePics/bridge56data.txt


A solution for 15 Bridge Tables (60 players)

Table 1    17 and 18  vs.  49 and 57
Table 2    56 and 58  vs.   2 and 29
Table 3    44 and 47  vs.   3 and 31
Table 4    46 and 50  vs.   9 and 25
Table 5    15 and 20  vs.  11 and 34
Table 6    42 and 48  vs.  41 and 51
Table 7    45 and 52  vs.  59 and  0
Table 8    13 and 22  vs.  14 and 35
Table 9    12 and 23  vs.   8 and 33
Table 10   43 and 55  vs.   7 and 26
Table 11   40 and 53  vs.   4 and 28
Table 12   10 and 24  vs.  16 and 36
Table 13   39 and 54  vs.  19 and 37
Table 14   21 and 38  vs.   5 and 27
Table 15    6 and 32  vs.   1 and 30

The starting positions for the first 100 cyclical Bridge/Whist Tournament Schedules for 60 players can be seen here.
http://www.durangobill.com/BridgePics/bridge60data.txt


A solution for 16 Bridge Tables (64 players)

Table 1    60 and 61  vs.  18 and 20
Table 2    49 and 52  vs.   3 and 33
Table 3    46 and 50  vs.  43 and 54
Table 4    48 and 53  vs.  10 and 26
Table 5    17 and 23  vs.  13 and 25
Table 6    15 and 22  vs.   9 and 27
Table 7    51 and 59  vs.   6 and 34
Table 8    47 and 56  vs.  16 and 38
Table 9    45 and 55  vs.  21 and 40
Table 10   62 and 12  vs.  11 and 36
Table 11   44 and 58  vs.  14 and 37
Table 12   42 and 57  vs.   7 and 28
Table 13   24 and 41  vs.   8 and 35
Table 14   19 and 39  vs.   4 and 30
Table 15    5 and 29  vs.   2 and 31
Table 16    1 and 32  vs.  63 and  0

The starting positions for the first 10 cyclical Bridge/Whist Tournament Schedules for 64 players can be seen here.
http://www.durangobill.com/BridgePics/bridge64data.txt


A solution for 17 Bridge Tables (68 players)

Table 1    65 and 66  vs.  49 and 60
Table 2    18 and 20  vs.   2 and 33
Table 3    50 and 53  vs.   6 and 36
Table 4    51 and 55  vs.  15 and 22
Table 5    52 and 57  vs.  54 and 63
Table 6    17 and 23  vs.  13 and 25
Table 7    56 and 64  vs.   7 and 30
Table 8    48 and 58  vs.  12 and 26
Table 9    46 and 59  vs.   1 and 34
Table 10   47 and 62  vs.   4 and 32
Table 11   45 and 61  vs.  19 and 41
Table 12   27 and 44  vs.  67 and  0
Table 13   10 and 28  vs.  21 and 42
Table 14   24 and 43  vs.   5 and 31
Table 15    9 and 29  vs.   8 and 37
Table 16   16 and 40  vs.   3 and 35
Table 17   14 and 39  vs.  11 and 38


A solution for 18 Bridge Tables (72 players)

Table 1    68 and 69  vs.  20 and 22
Table 2    55 and 58  vs.  52 and 57
Table 3    56 and 60  vs.   7 and 32
Table 4    17 and 23  vs.   5 and 33
Table 5    18 and 25  vs.  50 and 63
Table 6    59 and 67  vs.   1 and 36
Table 7    53 and 62  vs.  49 and 64
Table 8    51 and 61  vs.  10 and 30
Table 9    15 and 26  vs.  19 and 43
Table 10   54 and 66  vs.  27 and 46
Table 11   70 and 13  vs.   4 and 34
Table 12   12 and 28  vs.  29 and 47
Table 13   48 and 65  vs.   6 and 38
Table 14   24 and 45  vs.   8 and 39
Table 15    9 and 31  vs.  16 and 42
Table 16   21 and 44  vs.   2 and 35
Table 17   14 and 41  vs.  71 and  0
Table 18   11 and 40  vs.   3 and 37


A solution for 19 Bridge Tables (76 players)

Table 1    73 and 74  vs.  20 and 22
Table 2    57 and 60  vs.  59 and 63
Table 3    56 and 61  vs.  52 and 66
Table 4    17 and 23  vs.  24 and 47
Table 5    18 and 25  vs.   4 and 36
Table 6    64 and 72  vs.  29 and 49
Table 7    62 and 71  vs.   7 and 34
Table 8    55 and 65  vs.  15 and 26
Table 9    58 and 70  vs.  14 and 43
Table 10   54 and 67  vs.   5 and 35
Table 11   13 and 28  vs.  21 and 46
Table 12   53 and 69  vs.   6 and 40
Table 13   51 and 68  vs.   2 and 37
Table 14   12 and 30  vs.  75 and  0
Table 15   31 and 50  vs.   9 and 33
Table 16   27 and 48  vs.  10 and 32
Table 17   19 and 45  vs.   3 and 39
Table 18   16 and 44  vs.   8 and 41
Table 19   11 and 42  vs.   1 and 38


A solution for 20 Bridge Tables (80 players)

Table 1    76 and 77  vs.  23 and 25
Table 2    60 and 63  vs.  20 and 28
Table 3    22 and 26  vs.  52 and 72
Table 4    57 and 62  vs.  24 and 49
Table 5    61 and 67  vs.  55 and 68
Table 6    58 and 65  vs.  79 and  0
Table 7    66 and 75  vs.  11 and 44
Table 8    64 and 74  vs.  27 and 50
Table 9    59 and 70  vs.   3 and 41
Table 10   18 and 30  vs.  21 and 48
Table 11   17 and 31  vs.   4 and 38
Table 12   54 and 69  vs.  53 and 71
Table 13   78 and 15  vs.  10 and 34
Table 14   56 and 73  vs.   5 and 37
Table 15   13 and 32  vs.   9 and 35
Table 16   12 and 33  vs.   8 and 43
Table 17   29 and 51  vs.  14 and 45
Table 18   19 and 47  vs.   2 and 39
Table 19    7 and 36  vs.  16 and 46
Table 20    6 and 42  vs.   1 and 40


A solution for 21 Bridge Tables (84 players) (Added on July 16, 2008)

Table 1    80 and 81  vs.  23 and 25
Table 2    79 and 82  vs.  63 and 68
Table 3    22 and 26  vs.  65 and 77
Table 4    64 and 70  vs.   2 and 40
Table 5    59 and 66  vs.  16 and 57
Table 6    61 and 69  vs.  62 and 76
Table 7    19 and 28  vs.  24 and 50
Table 8    20 and 30  vs.   6 and 43
Table 9    67 and 78  vs.  55 and 72
Table 10   58 and 71  vs.   5 and 38
Table 11   60 and 75  vs.  12 and 34
Table 12   15 and 31  vs.  32 and 53
Table 13   56 and 74  vs.  10 and 35
Table 14   54 and 73  vs.   8 and 44
Table 15   13 and 33  vs.  21 and 49
Table 16   29 and 52  vs.   4 and 39
Table 17   27 and 51  vs.  83 and  0
Table 18    9 and 36  vs.  18 and 47
Table 19    7 and 37  vs.   1 and 41
Table 20   17 and 48  vs.  14 and 46
Table 21   11 and 45  vs.   3 and 42


A solution for 22 Bridge Tables (88 players) (Added on July 20, 2008)
 
Table 1    84 and 85  vs.  66 and 68
Table 2    25 and 28  vs.  22 and 26
Table 3    65 and 70  vs.  63 and 71
Table 4    67 and 73  vs.   8 and 46
Table 5    23 and 30  vs.  64 and 78
Table 6    74 and 83  vs.   7 and 50
Table 7    72 and 82  vs.  87 and  0
Table 8    20 and 31  vs.  27 and 54
Table 9    69 and 81  vs.  29 and 55
Table 10   62 and 75  vs.  13 and 36
Table 11   18 and 33  vs.   4 and 41
Table 12   61 and 77  vs.  15 and 34
Table 13   59 and 76  vs.   5 and 40
Table 14   86 and 17  vs.  14 and 48
Table 15   60 and 80  vs.  10 and 38
Table 16   58 and 79  vs.  16 and 49
Table 17   35 and 57  vs.   6 and 45
Table 18   32 and 56  vs.   1 and 43
Table 19   12 and 37  vs.   2 and 42
Table 20   24 and 53  vs.   3 and 44
Table 21    9 and 39  vs.  21 and 52
Table 22   19 and 51  vs.  11 and 47


A solution for 23 Bridge Tables (92 players) (Added on Aug. 16, 2008)

Table 1    89 and 90  vs.  68 and 70
Table 2    25 and 28  vs.  69 and 73
Table 3    72 and 77  vs.  67 and 75
Table 4    20 and 26  vs.  76 and 87
Table 5    23 and 30  vs.  29 and 57
Table 6    22 and 31  vs.  74 and 86
Table 7    78 and 88  vs.  62 and 82
Table 8    66 and 79  vs.   4 and 44
Table 9    71 and 85  vs.  13 and 38
Table 10   18 and 33  vs.   5 and 43
Table 11   64 and 80  vs.  35 and 59
Table 12   17 and 34  vs.   9 and 41
Table 13   63 and 81  vs.   2 and 45
Table 14   65 and 84  vs.  16 and 52
Table 15   15 and 36  vs.  19 and 53
Table 16   61 and 83  vs.   1 and 46
Table 17   37 and 60  vs.   6 and 48
Table 18   32 and 58  vs.  24 and 55
Table 19   12 and 39  vs.  11 and 50
Table 20   27 and 56  vs.   7 and 42
Table 21   10 and 40  vs.   8 and 49
Table 22   21 and 54  vs.   3 and 47
Table 23   14 and 51  vs.  91 and  0


A solution for 24 Bridge Tables (96 players) (Added on Aug. 22, 2010)

Table 1    92 and 93  vs.  28 and 30
Table 2    91 and 94  vs.  70 and 74
Table 3    22 and 27  vs.  69 and 75
Table 4    71 and 78  vs.  79 and 90
Table 5    23 and 31  vs.   1 and 47
Table 6    80 and 89  vs.  25 and 57
Table 7    67 and 77  vs.  11 and 51
Table 8    76 and 88  vs.  63 and 83
Table 9    20 and 33  vs.  72 and 24
Table 10   73 and 87  vs.  35 and 60
Table 11   66 and 81  vs.  37 and 61
Table 12   18 and 34  vs.  17 and 36
Table 13   65 and 82  vs.   5 and 44
Table 14   68 and 86  vs.  32 and 59
Table 15   64 and 85  vs.   4 and 45
Table 16   62 and 84  vs.  26 and 56
Table 17   15 and 38  vs.  12 and 40
Table 18   13 and 39  vs.   2 and 46
Table 19   29 and 58  vs.   7 and 43
Table 20   10 and 41  vs.  95 and  0
Table 21    9 and 42  vs.  19 and 54
Table 22   21 and 55  vs.   6 and 49
Table 23   16 and 53  vs.   8 and 50
Table 24   14 and 52  vs.   3 and 48


A solution for 25 Bridge Tables (100 players) (Added on June 29, 2016)
 
Table 1    96 and 97  vs.  26 and 28
Table 2    72 and 75  vs.  94 and 98
Table 3    71 and 76  vs.  74 and 80
Table 4    23 and 30  vs.  70 and 78
Table 5    22 and 31  vs.  77 and 91
Table 6    25 and 35  vs.  15 and 40
Table 7    82 and 93  vs.  64 and 88
Table 8    83 and 95  vs.  10 and 43
Table 9    79 and 92  vs.  18 and 38
Table 10   69 and 84  vs.   2 and 48
Table 11   20 and 36  vs.   4 and 47
Table 12   73 and 90  vs.   7 and 45
Table 13   67 and 85  vs.  29 and 60
Table 14   68 and 87  vs.  99 and  0
Table 15   65 and 86  vs.   8 and 52
Table 16   17 and 39  vs.  19 and 56
Table 17   66 and 89  vs.  32 and 81
Table 18   37 and 63  vs.   1 and 49
Table 19   34 and 61  vs.  12 and 42
Table 20   13 and 41  vs.  14 and 54
Table 21   33 and 62  vs.   9 and 44
Table 22   27 and 59  vs.   3 and 50
Table 23   24 and 58  vs.  21 and 57
Table 24   16 and 55  vs.   6 and 51
Table 25    5 and 46  vs.  11 and 53




Spouse avoidance schedules
   Any schedule involving 4N players (4, 8, 12, 16 . . .) or player vs. player round robin schedules (bottom of this page) can be used as a “spouse avoidance” schedule by simply matching spouses as partners (for 4N-player games) or opponents (for player vs. player games) for a “pretend” round 1. Then instead of playing the round, players simply start the cycle sequence by advancing to round 2. We note that in all configurations, each player plays opposite each other player once, and this “once” is disposed of in the “pretend” round.




   The table below shows some of the combinatorics associated with the round-robin problem. If you are going to have a tournament without someone sitting out part of the time, the number of players must be a multiple of four. In each game each player has a partner. Thus the number of teams is exactly one half of the number of players. A Bridge table has 4 positions for the players (Usually referred to as: North, East, South, and West). Hence the number of tables is one-quarter the number of players.

 
Notes: The number of solutions (1, 6, 20, 128, 1710, 81576, 7910127) has been added to “The On-Line Encyclopedia of Integer Sequences” http://oeis.org/A114959
The 1, 3, 25, 631, etc. under Qualifying Nbr Teams are the 1st, 3rd, 5th, 7th, etc. terms found at http://oeis.org/A006204
Please see the “Enumeration of “Starters”” section at the bottom of the page for more information.
Also see: Classification of Starters
http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.168.2315&rep=rep1&type=pdf


   If there were no constraints regarding the seating arrangements for 96 players, you could fill the first table position with any of 96 player-positions, the second table position with any of the remaining 95 player-positions, etc. for all 96 positions. The number of possible permutations is thus “NbrPlayers” Factorial. By the time you get to 96 players, the result is billions of times larger than the number of atoms in the known universe. How can I claim this when no one has counted the number of atoms in the known universe? Practical answer: “Pick a number” - any number you want, for the number of atoms in the known universe.

   The actual definition of a Bridge game requires that a player-position must have a specified partner-position who sits on the far side of a Bridge table. Thus the positions for the partners are paired to form teams. For the solution of the round-robin problem, one team combination is defined and held as a constant while the other team positions are allowed to float. In the diagram below which shows combinations for 8 players, position “0” is always paired with position “7”. In general, if there are “N” players involved, then the player-positions are identified by the digits from “0” to “N-1”. Position “0” is always teamed with position “N-1”


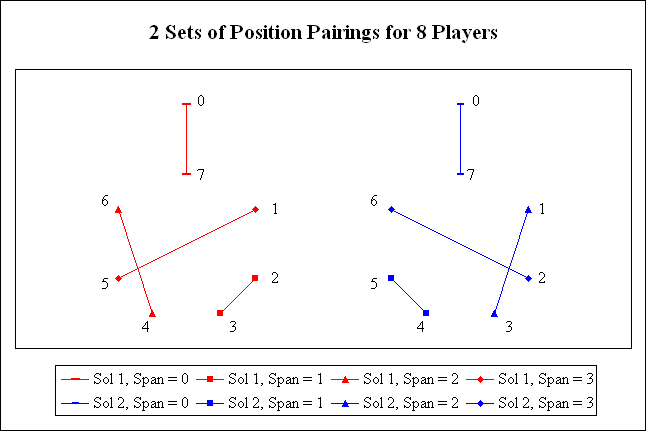
   In the diagram above, note how player-positions 1 to 7 are on the circumference of a circle while position “0” is “fixed” outside the circle. The diagram shows 2 different ways that an 8-player tournament can be paired into teams. If there were no restrictions on pairing combinations, then you could arbitrarily connect any two of the player/positions. Since we have already isolated two players (In this case, positions “0” and “7”), the total number of player-positions to be paired is 2 less than “NbrPlayers”, which can be done in FACT(NbrPlayers-2) ways. There would be considerable duplication of these pairings as the teams could be permuted in FACT(NbrTeams-1) ways. Thus we divide FACT(NbrPlayers-2) by FACT(NbrTeams-1) ways to adjust for permutations of team positions. Finally, each team could swap the position of the partners (north to south or east to west). We divide again by 2^(NbrTeams-1) which gives us the theoretical number of ways the player-positions could be matched into teams.

   However, the round-robin solution requires that each player must have each other player as a partner exactly once. In our diagram, this will only happen if we can pair all the players in a way that results in each line having a different span length (chord distance). The player-position from “0” to “7” has a defined length of “0”. (In any size diagram, the line connecting position “0” with position “N-1” will always have a length of zero.) In the left diagram above (red lines), the line connecting position “2” to position “3” has a length of “1”. Similarly, the line connecting “4” and “6” has a length of “2”. Finally, the line connecting “1” to “5” has a length of “3”. (Note: This is a “Shortest chord” length.) The blue lines show a symmetrically similar solution. Both of these diagrams lead to solutions to the round-robin tournament problem. There is still a third combination to connect the player-positions such that all lengths are different. (See if you can find it.)

   One of the tasks of the computer program is to generate these connections. The program also counts them as they are found. It found 3 of these for the 8-player problem, 25 for the 12-player problem, etc. By the time the computer program got to 28 players, it found 128,102,625 different ways to match player positions such that each player would have each other player as a partner exactly once.

   The next step in the computer program was to permute each of the above qualifying team candidates among the tables to see if each player will have each other player as an opponent exactly twice. For this, we use the above distance diagram again with the additional definition that all distances between any position and position “0” are defined as 0. We then match all opponent combinations to see if each distance occurs exactly twice.

(There are color coded diagrams near the bottom of the page that illustrates this two-step matching process, but for the 13 player, 4N+1 problem.)

As an example, let’s use the left (red) solution of:
2 and 3 vs. 4 and 6     5 and 1 vs. 7 and 0
for the 8-player problem.

If we tabulate the opponents and distances for “2 and 3 vs. 4 and 6”, we have the following opponent matches and distances:
2 to 4, dist = 2
2 to 6, dist = 3
3 to 4, dist = 1
3 to 6, dist = 3

Similarly, “5 and 1  vs.  7 and 0” yields:
5 to 7, dist = 2
5 to 0, dist = 0
1 to 7, dist = 1
1 to 0, dist = 0

In the above listing, each of the distances (0, 1, 2, 3) occurred exactly twice. Thus,
2 and 3 vs. 4 and 6    5 and 1 vs. 7 and 0
is a valid solution to the round-robin problem. It turns out that both of the other two permutations of these teams also pass the “opponent” test. Solutions 1, 2 and 3 (see the list for 8-player solutions above) are team permutations of the “Red” diagram. The “Blue” diagram supplies 3 more solutions to the 8-player problem. As mentioned earlier, there is still another “pairing” of the positions 1 through 6. However, this candidate did not pass the above “opponent” test.

   By the time the problem was expanded to 28 players, the computer found 128,102,625 different ways of pairing the players such that each chord distance was different. Each of these 128,102,625 candidates was then run through a search tree that has 135,135 different permutations to see if a total solution existed. 7,910,127 of these yielded valid position definitions that solve a round robin tournament for 28 players. This effort can be affectionately described as “Computationally intensive”.

   For larger numbers of players, the search was cut short after a single solution was found. The search algorithm prunes off branches whenever possible, but there is a limit to what computers can do.

   Finally, the computer program has a “verify” function that sequences players through the positions as shown for the 8-player and 12-player solutions. This was done just to double check that everything was valid. All solutions shown here passed this “double check” test.




   A related round-robin scheduling problem involves sequencing tournament play for fixed teams. This would apply when the individuals in each team form a permanent partnership, but you wish to schedule team play so that each team plays against each other team exactly once. The algorithm/scheduling sequence given below will also work for any single-player game where each player plays against each other player exactly once. Examples would include chess, singles tennis, any player-vs.-player game, any team-vs.-team game, etc.

   The algorithm will work for any number of teams. The example shown below has an even number of teams, but if you have an odd number, just add a “dummy” team named “Bye” to make the total come out even. Anyone who plays against “Bye” gets an automatic win for that round.

   The example uses 8 teams. If you have more (or less) than 8 teams, just extend (or shorten) the length of the columns as needed. Team positions are defined by the digits 0 to 7. Two columns are used with the digits 1 to 4 in the right column. The left column has the remaining digits (5-7) plus a “0” at the top. If you have a larger number of teams, simply extend the columns. For example, if you have 20 teams, the right column would have the numbers from 1 to 10 while the left column would work up from 11 to 19 with a “0” at the top.

0  vs.  1
7  vs.  2
6  vs.  3
5  vs.  4

Initially, teams may be assigned to the 8 positions in any random order. For our example:
Team A is at position 0
Team B is at position 1
Team C is at position 2
Team D is at position 3
Team E is at position 4
Team F is at position 5
Team G is at position 6
Team H is at position 7

   For each round of play, the team that is at position 0 plays against the team at position 1, etc. for each row of the diagram. Thus, first round opponents are:
Team A (at position 0) plays against Team B (at position 1)
Team H (at position 7) plays against Team C (at position 2)
Team G (at position 6) plays against Team D (at position 3)
Team F (at position 5) plays against Team E (at position 4)

   For the next round, the teams move as follows: Whoever was at position “0” stays there. (In fact the team at “0” stays there for the entire tournament.) All other teams advance one position except for the team at “7” which cycles back to position “1”. Thus for round 2:
Team A stays at position 0
Team B moves from position 1 to position 2
Team C moves from position 2 to position 3
Team D moves from position 3 to position 4
Team E moves from position 4 to position 5
Team F moves from position 5 to position 6
Team G moves from position 6 to position 7
Team H moves from position 7 to position 1

The opponents for round 2 thus become:
Team A (at position 0) plays against Team H (at position 1)
Team G (at position 7) plays against Team B (at position 2)
Team F (at position 6) plays against Team C (at position 3)
Team E (at position 5) plays against Team D (at position 4)

   For each subsequent round of play, Team A stays at position “0”. All other teams advance one position. The sequence is somewhat like a circular conveyor belt. A more accurate name for the process is “cyclic solution”, but it is easier to think of it as a circular conveyor belt moving along an assembly line. After 7 rounds, each team will have played against each other team exactly once. If you have 20 teams then 19 rounds will be required.

   At each position on the moving assembly line “something” happens. The “something” is that whoever is at this position is matched against whoever is in the “return” position of the conveyor belt going in the other direction. The sequence will match each team against each other team exactly once, and will work for any number of positions provided the number of positions on the moving belt is an odd number. The requirement for an “odd number” of positions along the moving belt is why position “0” is defined as a stationary position. If we start with an “even” number of positions and “freeze” position “0”, we will be left with an odd number for the teams that move.

   Finally, we can ask the question: Is there more than one way to schedule a Round Robin tournament such that each team plays against each other team once (or each single player plays against each other player once)? The answer is “Yes”. For how many ways this can be done, please see the “Player vs. Player (or Team vs. Team) Combinatorics” section near the end of this page.




   It’s also possible to schedule a tournament for 4N + 1 players. (N = number of tables and the number of players can equal 5, 9, 13, 17, etc.) In this case there is one extra player so one person will sit out each round. However, by the time that all rounds have been played, each person will have had each other person as a partner once and as an opponent twice.

   In the 4N player combinations (solutions given above), one person stays at the zero location and all other players cycle to the next position on each succeeding round. In the schedules for 4N + 1 players, everyone cycles to the next position on each round, but whoever is at position “0” is the extra person who doesn’t play in the particular round.






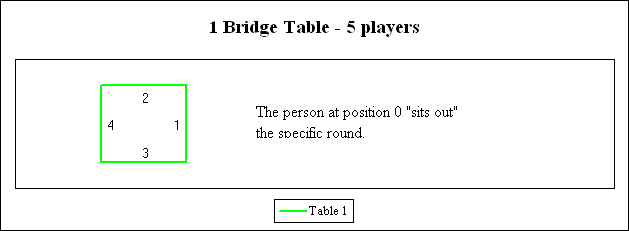
   The diagram above shows the only cyclical solution for 5 players. The 5 players (A, B, C, D, E) initially start at the 5 positions 2, 3, 4, 1, 0. The players at positions 1 - 4 play a normal round while the person at position 0 “sits out” the round. After the first round is over, each player advances to the next highest position, except the player who was at position 4 cycles to position 0. The people at positions 1 - 4 again play a normal round. The sequence continues for 5 rounds.  (Number of players = Number of rounds)

The table below shows the position for each player for each round.

Round   Player  Player  Player  Player  Player
 Nbr.     A       B       C       D       E
  1       2       3       4       1       0
  2       3       4       0       2       1
  3       4       0       1       3       2
  4       0       1       2       4       3
  5       1       2       3       0       4

At the end of 5 rounds of play, each player has had each other player as a partner once and as an opponent twice.

The shorthand summary for this solution is:

Solution    <---- Table 1 ---->
   1        2 and 3 vs. 4 and 1




   There are 9 possible team matching patterns such that each player would have each other player as a partner once, but unfortunately, there are no combinations that produce a cyclical solution.

   Non cyclical solutions for 9 players exist. The following schedule for 9 players (A to I) is adapted from http://www.jdawiseman.com/papers/tournaments/individual-pairs/ip-pure_09.html

         Sits         Table             Table
Round    Out            1                 2
  1       A      B & C vs D & G     E & I vs F & H
  2       B      C & A vs E & H     F & G vs D & I
  3       C      A & B vs F & I     D & H vs E & G
  4       D      E & F vs G & A     H & C vs I & B
  5       E      F & D vs H & B     I & A vs G & C
  6       F      D & E vs I & C     G & B vs H & A
  7       G      H & I vs A & D     B & F vs C & E
  8       H      I & G vs B & E     C & D vs A & F
  9       I      G & H vs C & F     A & E vs B & D



   There are 133 possible team matching patterns such that each player would have each other player as a partner once. These can be matched into 9 table combinations that would let each player have each other player as an opponent twice.

The diagram below shows the starting positions for one of the nine solutions.


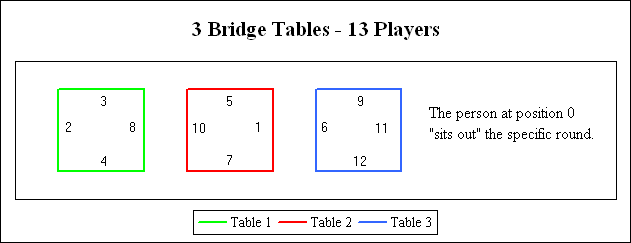
   The solution for 13 players shows the 12 Bridge-table positions plus position 0 for the player who “sits out” the current round. The table below shows the position for each of the 13 players (A to M) for each round of play.

Round  Plr Plr Plr Plr   Plr Plr Plr Plr   Plr Plr Plr Plr   Plr
 Nbr    A   B   C   D     E   F   G   H     I   J   K   L     M
  1     3   4   2   8     5   7  10   1     9  12   6  11     0
  2     4   5   3   9     6   8  11   2    10   0   7  12     1
  3     5   6   4  10     7   9  12   3    11   1   8   0     2
  4     6   7   5  11     8  10   0   4    12   2   9   1     3
  5     7   8   6  12     9  11   1   5     0   3  10   2     4
  6     8   9   7   0    10  12   2   6     1   4  11   3     5
  7     9  10   8   1    11   0   3   7     2   5  12   4     6
  8    10  11   9   2    12   1   4   8     3   6   0   5     7
  9    11  12  10   3     0   2   5   9     4   7   1   6     8
 10    12   0  11   4     1   3   6  10     5   8   2   7     9
 11     0   1  12   5     2   4   7  11     6   9   3   8    10
 12     1   2   0   6     3   5   8  12     7  10   4   9    11
 13     2   3   1   7     4   6   9   0     8  11   5  10    12


The shorthand summary for this solution is:

Solution  <----- Table 1 ----->   <----- Table 2 ----->   <----- Table 3 ----->
   1      3 and 4  vs.  2 and 8   5 and 7  vs. 10 and 1   9 and 12 vs. 6 and 11


The diagrams below show the graphical representation of this solution.


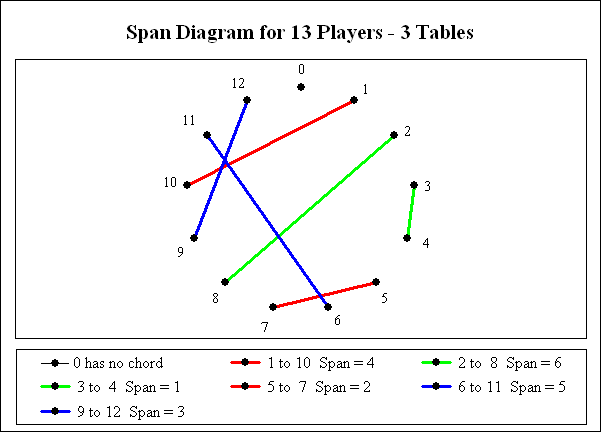
   The first step in the solution process is to match player positions so they form teams. Vertices representing player positions are placed around the circumference of a circle. Then chords are drawn to connect positions into teams such that each chord has a different length. The solid lines in the above graph identify team partnerships. The color coding will become significant in the next diagram.


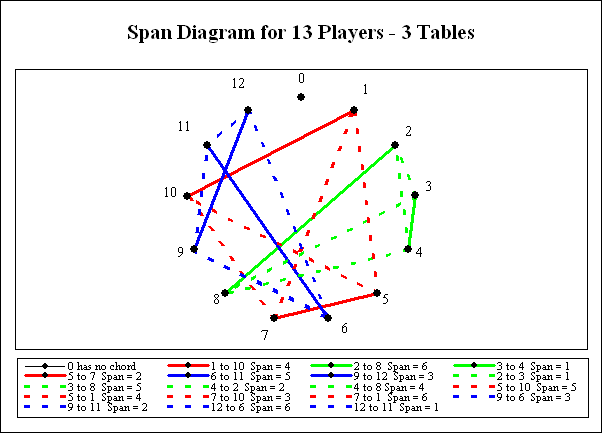
   After the positions have been matched into teams, the teams have to be matched into tables. Teams are matched so that all of the opponent chord distances (dashed lines) are used exactly twice.

   Almost all patterns have a mirror image. (The few exceptions are their own mirror images.) The two diagrams below show the span diagrams for the mirror image of the above solution.


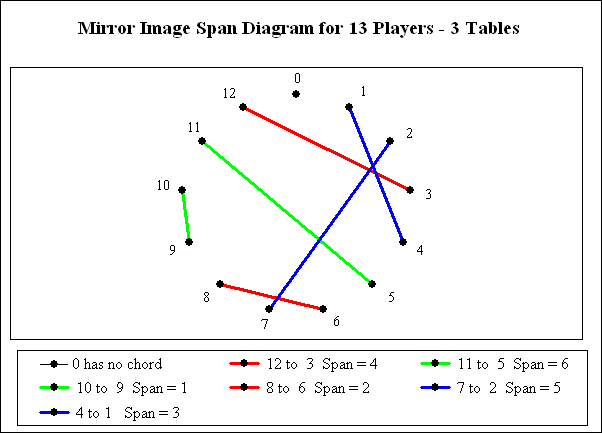
The above diagram shows the mirror image of matching player positions to form teams.



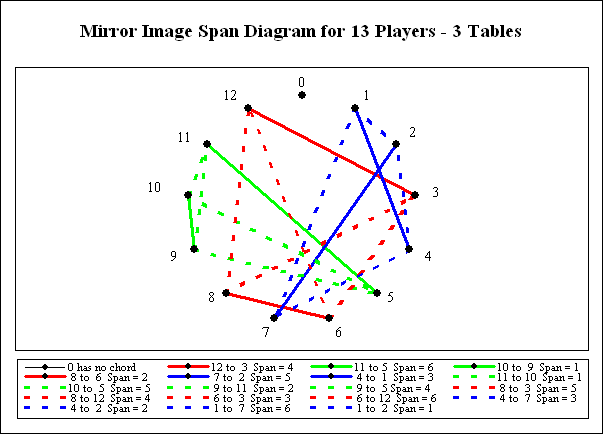
The above diagram shows the mirror image of matching teams into tables.

   If you take advantage of mirror images, it cuts the run time for the computer program by a factor of two. This is most helpful when counting solutions for higher orders of “N” for both the 4N and the 4N+1 problems.


   There is no easy way to match positions into teams or to match teams into tables. All possible combinations have to be generated by brute force trial and error. (This is where computers are a great help. Computers are really good at brute force trial and error.) Note: The algorithm and diagrams for “4N” players are similar this “4N+1” method.


There are 8 other solutions for 13 players. The table below shows the starting positions for these solutions.

Solution  <----- Table 1 ----->   <----- Table 2 ----->   <----- Table 3 ----->
   2       9 & 10  vs.   5 &  7    1 &  4  vs.   2 &  8   12 &  3  vs.   6 & 11
   3       3 &  4  vs.   6 &  8    9 & 12  vs.   5 & 11   10 &  1  vs.   2 &  7
   4       9 & 10  vs.   5 & 11    6 &  8  vs.  12 &  3    1 &  4  vs.   2 &  7
   5       4 &  5  vs.   7 &  9   12 &  2  vs.   8 &  1    6 & 10  vs.  11 &  3
   6      10 & 11  vs.   9 &  2    3 &  5  vs.   8 & 12    4 &  7  vs.   1 &  6
   7       6 &  7  vs.   4 &  9   12 &  1  vs.   5 &  8   11 &  2  vs.  10 &  3
   8       2 &  3  vs.  11 &  4    8 & 10  vs.   1 &  5    6 &  9  vs.   7 & 12
   9       8 &  9  vs.   4 &  6   11 &  1  vs.  12 &  5    3 &  7  vs.  10 &  2




   There are 3,857 possible team matching patterns such that each player would have each other player as a partner once. These can be matched into 179 table combinations that would let each player have each other player as an opponent twice.

   Rapidly increasing numbers of solutions exist for all larger numbers of players. The solution below defines a table-position numbering system that will allow each player to have each other player as a partner once and as an opponent twice. Players can be seated randomly, and thereafter sequence/cycle as in the earlier examples.

Table 1    14 and 15  vs.   2 and  4
Table 2     5 and  8  vs.   7 and 13
Table 3    12 and 16  vs.   1 and  9
Table 4     6 and 11  vs.   3 and 10

The starting positions for all 179 cyclical Bridge/Whist Tournament Schedules for 17 players can be seen here.
http://www.durangobill.com/BridgePics/bridge17data.txt


A solution for 21 players (Selected from a total of 3,900 solutions)

   There are 188,181 possible team matching patterns such that each player would have each other player as a partner once. These can be matched into 3,900 table combinations that would let each player have each other player as an opponent twice.

Table 1     9 and 10  vs.   4 and  7
Table 2    15 and 17  vs.   8 and 16
Table 3     2 and  6  vs.  13 and 18
Table 4    14 and 20  vs.   3 and 12
Table 5    19 and  5  vs.   1 and 11

The starting positions for all 3,900 cyclical Bridge/Whist Tournament Schedules for 21 players can be seen here.
http://www.durangobill.com/BridgePics/bridge21data.txt


A solution for 25 players (Selected from a total of 215,175 solutions)

   There are 13,376,125 possible team matching patterns such that each player would have each other player as a partner once. These can be matched into 215,175 table combinations that would let each player have each other player as an opponent twice.

Table 1     5 and  6  vs.   1 and 13
Table 2    20 and 22  vs.  11 and 19
Table 3    21 and 24  vs.   2 and 12
Table 4     4 and  8  vs.  18 and 23
Table 5     9 and 15  vs.  10 and 17
Table 6     7 and 16  vs.   3 and 14

The starting positions for the first 1,000 cyclical Bridge/Whist Tournament Schedules for 25 players can be seen here.
http://www.durangobill.com/BridgePics/bridge25data.txt


A solution for 29 players (Selected from a total of 21,500,927 solutions)

   There are 1,317,606,101 possible team matching patterns such that each player would have each other player as a partner once. These can be matched into 21,500,927 table combinations that would let each player have each other player as an opponent twice.

Table 1    24 and 25  vs.   7 and 11
Table 2    20 and 22  vs.   1 and 15
Table 3     9 and 12  vs.   8 and 18
Table 4    23 and 28  vs.   2 and 14
Table 5    21 and 27  vs.  26 and  4
Table 6     5 and 13  vs.   3 and 16
Table 7    10 and 19  vs.   6 and 17

The starting positions for the first 1,000 cyclical Bridge/Whist Tournament Schedules for 29 players can be seen here.
http://www.durangobill.com/BridgePics/bridge29data.txt


A solution for 33 players (Selected from a total of 3,488,427,990 solutions)

Table 1    29 and 30  vs.  13 and 22
Table 2    26 and 28  vs.   8 and 20
Table 3     9 and 12  vs.   7 and 14
Table 4    23 and 27  vs.   1 and 17
Table 5     5 and 10  vs.   6 and 19
Table 6    25 and 31  vs.   2 and 16
Table 7    24 and 32  vs.  11 and 21
Table 8     4 and 15  vs.   3 and 18

The starting positions for the first 1,000 cyclical Bridge/Whist Tournament Schedules for 33 players can be seen here.
http://www.durangobill.com/BridgePics/bridge33data.txt


A solution for 37 players

Table 1    13 and 14  vs.  10 and 12
Table 2    26 and 29  vs.   7 and 15
Table 3    30 and 34  vs.   2 and 18
Table 4    27 and 32  vs.   4 and 17
Table 5    25 and 31  vs.   1 and 19
Table 6    28 and 35  vs.  36 and  9
Table 7    24 and 33  vs.   3 and 20
Table 8     5 and 16  vs.   8 and 22
Table 9    11 and 23  vs.   6 and 21

The starting positions for the first 1,000 cyclical Bridge/Whist Tournament Schedules for 37 players can be seen here.
http://www.durangobill.com/BridgePics/bridge37data.txt


A solution for 41 players

Table 1    32 and 33  vs.   6 and 23
Table 2    13 and 15  vs.  14 and 26
Table 3     9 and 12  vs.  28 and 36
Table 4    35 and 39  vs.  30 and 37
Table 5    29 and 34  vs.   8 and 24
Table 6    10 and 16  vs.   3 and 22
Table 7    31 and 40  vs.   2 and 20
Table 8     7 and 17  vs.  11 and 25
Table 9    27 and 38  vs.   4 and 19
Table 10    5 and 18  vs.   1 and 21

The starting positions for the first 1,000 cyclical Bridge/Whist Tournament Schedules for 41 players can be seen here.
http://www.durangobill.com/BridgePics/bridge41data.txt


A solution for 45 players

Table 1    12 and 13  vs.  14 and 28
Table 2    34 and 36  vs.   1 and 23
Table 3    15 and 18  vs.  32 and 37
Table 4    38 and 42  vs.   2 and 22
Table 5    33 and 39  vs.   7 and 19
Table 6    10 and 17  vs.  44 and  9
Table 7    35 and 43  vs.  31 and 40
Table 8    30 and 41  vs.   3 and 24
Table 9    16 and 29  vs.   8 and 26
Table 10    5 and 20  vs.  11 and 27
Table 11    4 and 21  vs.   6 and 25

The starting positions for the first 1,000 cyclical Bridge/Whist Tournament Schedules for 45 players can be seen here.
http://www.durangobill.com/BridgePics/bridge45data.txt


A solution for 49 players

Table 1    12 and 13  vs.   7 and 21
Table 2    15 and 17  vs.  38 and 47
Table 3    36 and 39  vs.  42 and 46
Table 4    35 and 40  vs.   6 and 27
Table 5    37 and 43  vs.   1 and 25
Table 6    41 and 48  vs.  10 and 18
Table 7    34 and 44  vs.   5 and 22
Table 8     9 and 20  vs.   4 and 23
Table 9    33 and 45  vs.  11 and 29
Table 10   19 and 32  vs.   8 and 28
Table 11   16 and 31  vs.  14 and 30
Table 12    2 and 24  vs.   3 and 26

The starting positions for the first 1,000 cyclical Bridge/Whist Tournament Schedules for 49 players can be seen here.
http://www.durangobill.com/BridgePics/bridge49data.txt


A solution for 53 players

Table 1    17 and 18  vs.  19 and 34
Table 2    13 and 15  vs.  40 and 44
Table 3    39 and 42  vs.   3 and 28
Table 4    46 and 51  vs.   2 and 26
Table 5    43 and 49  vs.  11 and 31
Table 6    38 and 45  vs.  16 and 33
Table 7    12 and 20  vs.  52 and 10
Table 8    41 and 50  vs.  37 and 47
Table 9    36 and 48  vs.   6 and 29
Table 10    9 and 22  vs.   4 and 25
Table 11   21 and 35  vs.   1 and 27
Table 12    7 and 23  vs.   8 and 30
Table 13   14 and 32  vs.   5 and 24

The starting positions for the first 1,000 cyclical Bridge/Whist Tournament Schedules for 53 players can be seen here.
http://www.durangobill.com/BridgePics/bridge53data.txt


A solution for 57 players

Table 1    55 and 56  vs.   8 and 32
Table 2    15 and 17  vs.  47 and 54
Table 3    45 and 48  vs.  44 and 53
Table 4    42 and 46  vs.   6 and 31
Table 5    13 and 18  vs.  16 and 35
Table 6    43 and 49  vs.  19 and 36
Table 7    12 and 20  vs.   5 and 26
Table 8    40 and 50  vs.   9 and 22
Table 9    41 and 52  vs.   3 and 30
Table 10   39 and 51  vs.  23 and 38
Table 11   10 and 24  vs.   1 and 29
Table 12   21 and 37  vs.  11 and 33
Table 13    7 and 25  vs.   4 and 27
Table 14   14 and 34  vs.   2 and 28

The starting positions for the first 1,000 cyclical Bridge/Whist Tournament Schedules for 57 players can be seen here.
http://www.durangobill.com/BridgePics/bridge57data.txt

 
A solution for 61 players

Table 1    45 and 46  vs.  44 and 49
Table 2    20 and 22  vs.  40 and 56
Table 3    15 and 18  vs.  10 and 25
Table 4    47 and 51  vs.  16 and 37
Table 5    17 and 23  vs.   8 and 34
Table 6    52 and 59  vs.  60 and 12
Table 7    50 and 58  vs.   9 and 26
Table 8    48 and 57  vs.  11 and 35
Table 9    43 and 53  vs.   1 and 31
Table 10   13 and 24  vs.  41 and 55
Table 11   42 and 54  vs.  14 and 36
Table 12   21 and 39  vs.   5 and 28
Table 13   19 and 38  vs.   3 and 32
Table 14    7 and 27  vs.   2 and 30
Table 15    4 and 29  vs.   6 and 33

The starting positions for the first 100 cyclical Bridge/Whist Tournament Schedules for 61 players can be seen here.
http://www.durangobill.com/BridgePics/bridge61data.txt


A solution for 65 players

Table 1    63 and 64  vs.  49 and 51
Table 2    50 and 53  vs.  46 and 56
Table 3    18 and 22  vs.  10 and 27
Table 4    15 and 20  vs.  45 and 60
Table 5    17 and 23  vs.  52 and 61
Table 6    48 and 55  vs.   1 and 33
Table 7    54 and 62  vs.  13 and 25
Table 8    47 and 58  vs.  16 and 39
Table 9    44 and 57  vs.   5 and 30
Table 10   12 and 26  vs.   8 and 36
Table 11   43 and 59  vs.  11 and 37
Table 12   24 and 42  vs.  19 and 40
Table 13    9 and 28  vs.   7 and 29
Table 14   21 and 41  vs.   2 and 32
Table 15   14 and 38  vs.   4 and 31
Table 16    6 and 35  vs.   3 and 34

The starting positions for the first 10 cyclical Bridge/Whist Tournament Schedules for 65 players can be seen here.
http://www.durangobill.com/BridgePics/bridge65data.txt


A solution for 69 players

Table 1    66 and 67  vs.  15 and 26
Table 2    20 and 22  vs.   3 and 36
Table 3    53 and 56  vs.  52 and 64
Table 4    54 and 58  vs.  48 and 61
Table 5    50 and 55  vs.   6 and 37
Table 6    17 and 23  vs.  24 and 44
Table 7    18 and 25  vs.  49 and 59
Table 8    57 and 65  vs.  12 and 28
Table 9    51 and 60  vs.  14 and 40
Table 10   68 and 13  vs.  46 and 63
Table 11   47 and 62  vs.   5 and 32
Table 12   27 and 45  vs.   1 and 35
Table 13   10 and 29  vs.   7 and 31
Table 14    9 and 30  vs.  21 and 43
Table 15   19 and 42  vs.   4 and 33
Table 16   16 and 41  vs.  11 and 39
Table 17    8 and 38  vs.   2 and 34


A solution for 73 players

Table 1    71 and 72  vs.  56 and 68
Table 2    20 and 22  vs.  60 and 69
Table 3    55 and 58  vs.  11 and 41
Table 4    57 and 61  vs.   9 and 32
Table 5    54 and 59  vs.  52 and 65
Table 6    17 and 23  vs.   2 and 36
Table 7    18 and 25  vs.  15 and 26
Table 8    62 and 70  vs.  13 and 28
Table 9    53 and 63  vs.  12 and 30
Table 10   50 and 64  vs.  14 and 42
Table 11   51 and 67  vs.   6 and 39
Table 12   49 and 66  vs.  29 and 48
Table 13   27 and 47  vs.   8 and 40
Table 14   10 and 31  vs.   1 and 37
Table 15   24 and 46  vs.  19 and 44
Table 16   21 and 45  vs.   4 and 35
Table 17    7 and 33  vs.   3 and 38
Table 18   16 and 43  vs.   5 and 34


A solution for 77 players

Table 1    75 and 76  vs.  59 and 61
Table 2    20 and 23  vs.  22 and 26
Table 3    57 and 62  vs.  19 and 46
Table 4    58 and 64  vs.  29 and 50
Table 5    18 and 25  vs.  63 and 73
Table 6    66 and 74  vs.  51 and 70
Table 7    56 and 65  vs.   7 and 35
Table 8    17 and 28  vs.  52 and 68
Table 9    60 and 72  vs.   8 and 41
Table 10   54 and 67  vs.  27 and 49
Table 11   55 and 69  vs.   1 and 38
Table 12   15 and 30  vs.   2 and 37
Table 13   14 and 31  vs.   6 and 40
Table 14   53 and 71  vs.  21 and 47
Table 15   12 and 32  vs.  11 and 42
Table 16   10 and 33  vs.  13 and 43
Table 17   24 and 48  vs.   4 and 36
Table 18    9 and 34  vs.  16 and 45
Table 19    3 and 39  vs.  44 and  5


A solution for 81 players

Table 1    78 and 79  vs.  24 and 26
Table 2    61 and 64  vs.  63 and 67
Table 3    20 and 25  vs.  56 and 74
Table 4    22 and 28  vs.   4 and 38
Table 5    59 and 66  vs.  29 and 52
Table 6    69 and 77  vs.  12 and 34
Table 7    62 and 71  vs.  23 and 49
Table 8    58 and 68  vs.  60 and 75
Table 9    65 and 76  vs.  80 and 15
Table 10   18 and 30  vs.  19 and 47
Table 11   57 and 70  vs.  14 and 45
Table 12   17 and 31  vs.   8 and 43
Table 13   55 and 72  vs.   6 and 42
Table 14   54 and 73  vs.  13 and 33
Table 15   32 and 53  vs.  50 and  9
Table 16   27 and 51  vs.   5 and 37
Table 17   10 and 35  vs.  16 and 46
Table 18   21 and 48  vs.   1 and 40
Table 19    7 and 36  vs.   3 and 41
Table 20   11 and 44  vs.   2 and 39


A solution for 85 players

Table 1    64 and 65  vs.  23 and 25
Table 2    80 and 83  vs.  22 and 26
Table 3    62 and 67  vs.  12 and 34
Table 4    63 and 69  vs.   4 and 40
Table 5    61 and 68  vs.  73 and 82
Table 6    20 and 28  vs.  11 and 46
Table 7    71 and 81  vs.  56 and 75
Table 8    59 and 70  vs.   3 and 43
Table 9    18 and 30  vs.  31 and 54
Table 10   66 and 79  vs.  13 and 33
Table 11   58 and 72  vs.  57 and 74
Table 12   17 and 32  vs.  24 and 51
Table 13   84 and 15  vs.   9 and 37
Table 14   60 and 78  vs.  16 and 48
Table 15   55 and 76  vs.   8 and 45
Table 16   29 and 53  vs.  21 and 50
Table 17   27 and 52  vs.   7 and 38
Table 18   10 and 36  vs.  14 and 47
Table 19   19 and 49  vs.   6 and 44
Table 20    5 and 39  vs.   2 and 41
Table 21    1 and 42  vs.  35 and 77


A solution for 89 players

Note: This solution uses a “patterned starter” where the positions for each team add to 89.

Table 1    44 and 45  vs.  43 and 46
Table 2    42 and 47  vs.  39 and 50
Table 3    41 and 48  vs.  37 and 52
Table 4    40 and 49  vs.  35 and 54
Table 5    38 and 51  vs.  23 and 66
Table 6    36 and 53  vs.  14 and 75
Table 7    34 and 55  vs.   9 and 80
Table 8    33 and 56  vs.   7 and 82
Table 9    32 and 57  vs.   2 and 87
Table 10   31 and 58  vs.  13 and 76
Table 11   30 and 59  vs.   3 and 86
Table 12   29 and 60  vs.   6 and 83
Table 13   28 and 61  vs.   8 and 81
Table 14   27 and 62  vs.  15 and 74
Table 15   26 and 63  vs.   5 and 84
Table 16   25 and 64  vs.  12 and 77
Table 17   24 and 65  vs.  17 and 72
Table 18   22 and 67  vs.  16 and 73
Table 19   21 and 68  vs.  11 and 78
Table 20   20 and 69  vs.   4 and 85
Table 21   19 and 70  vs.  10 and 79
Table 22   18 and 71  vs.   1 and 88


A solution for 93 players

The following solution was originally published in a paper by Julian Abel, Frank Bennett and Gennian Ge titled “Existence of Directed Triplewhist Tournaments with the Three Person Property 3PDTWh(v)”, and forwarded to me by Norman Finizio. Also note that there are no “patterned solutions” for Wh(93) or any other number that is +/- 12, 24, 36, etc. of Wh(93).

Table 1    58 and 74  vs.  21 and 65
Table 2    32 and 23  vs.  20 and 86
Table 3    82 and 18  vs.  84 and 52
Table 4    55 and  5  vs.  83 and 46
Table 5    53 and 67  vs.  59 and 89
Table 6    70 and 39  vs.  22 and 12
Table 7    66 and 14  vs.  27 and 35
Table 8    11 and 80  vs.  61 and 79
Table 9    77 and 37  vs.  69 and 72
Table 10   51 and 85  vs.  13 and 28
Table 11   60 and 56  vs.  78 and 31
Table 12   64 and  6  vs.  50 and 38
Table 13   43 and 41  vs.  40 and 45
Table 14   26 and  9  vs.  33 and 71
Table 15   92 and 19  vs.  75 and  3
Table 16   63 and 91  vs.  48 and 49
Table 17    7 and 30  vs.  90 and 54
Table 18    8 and 47  vs.  81 and 36
Table 19   16 and 87  vs.  76 and 34
Table 20    4 and 29  vs.  17 and 10
Table 21   88 and  1  vs.  42 and 68
Table 22   62 and 73  vs.  57 and 24
Table 23   25 and 44  vs.   2 and 15


A solution for 97 players

Note: This solution uses a “patterned starter” where the positions for each team add to 97.

Table 1    48 and 49  vs.  47 and 50
Table 2    46 and 51  vs.  43 and 54
Table 3    45 and 52  vs.  41 and 56
Table 4    44 and 53  vs.  39 and 58
Table 5    42 and 55  vs.  32 and 65
Table 6    40 and 57  vs.  18 and 79
Table 7    38 and 59  vs.  12 and 85
Table 8    37 and 60  vs.   7 and 90
Table 9    36 and 61  vs.   5 and 92
Table 10   35 and 62  vs.  11 and 86
Table 11   34 and 63  vs.   2 and 95
Table 12   33 and 64  vs.  16 and 81
Table 13   31 and 66  vs.   6 and 91
Table 14   30 and 67  vs.   3 and 94
Table 15   29 and 68  vs.  14 and 83
Table 16   28 and 69  vs.  10 and 87
Table 17   27 and 70  vs.  15 and 82
Table 18   26 and 71  vs.  19 and 78
Table 19   25 and 72  vs.   9 and 88
Table 20   24 and 73  vs.   4 and 93
Table 21   23 and 74  vs.  17 and 80
Table 22   22 and 75  vs.  13 and 84
Table 23   21 and 76  vs.   8 and 89
Table 24   20 and 77  vs.   1 and 96


A solution for 101 players

Note: This solution uses a “patterned starter” where the positions for each team add to 101.

Table 1    50 and 51  vs.  49 and 52
Table 2    48 and 53  vs.  45 and 56
Table 3    47 and 54  vs.  43 and 58
Table 4    46 and 55  vs.  41 and 60
Table 5    44 and 57  vs.  37 and 64
Table 6    42 and 59  vs.  20 and 81
Table 7    40 and 61  vs.  14 and 87
Table 8    39 and 62  vs.  11 and 90
Table 9    38 and 63  vs.   7 and 94
Table 10   36 and 65  vs.   2 and 99
Table 11   35 and 66  vs.   5 and 96
Table 12   34 and 67  vs.   9 and 92
Table 13   33 and 68  vs.  15 and 86
Table 14   32 and 69  vs.   3 and 98
Table 15   31 and 70  vs.  18 and 83
Table 16   30 and 71  vs.   6 and 95
Table 17   29 and 72  vs.  17 and 84
Table 18   28 and 73  vs.  13 and 88
Table 19   27 and 74  vs.  10 and 91
Table 20   26 and 75  vs.  16 and 85
Table 21   25 and 76  vs.  19 and 82
Table 22   24 and 77  vs.   8 and 93
Table 23   23 and 78  vs.   4 and 97
Table 24   22 and 79  vs.   1 and 100
Table 25   21 and 80  vs.  12 and 89



The table below gives some of the combinatorics for the 4N + 1 scheduling problem.


Note: The 1, 9, 133, 3857, etc. “Qualifying Nbr. Teams” are the 2nd, 4th, 6th, 8th, etc. terms found at http://oeis.org/A006204
Please see the “Enumeration of “Starters”” section at the bottom of the page for more information.





   In the scheduling solutions given above, each player has each other as a partner once and as an opponent twice. However, there wasn’t any definition regarding “left” or “right” opponents. For example, an opponent could be:
1)  To the left of the player on both occasions.
2)  To the right of the player on both occasions.
3)  Or once to the left and once to the right.

A “directed” whist tournament schedule further restricts the schedules to just those where each player has each other player:
1)  As left opponent once.
2)  As a partner once.
3)  And as a right opponent once.

There are no cyclical directed whist schedules for the “4N” groups. (Number of players = 4, 8, 12, 16, 20, 24, 28, etc.)
(Personal correspondence with Norman Finizio. -  http://www.math.uri.edu/~finizio/finizio.html )
The closest possible directed schedules for 4N players are given in the “(Almost) Directed Solutions for 4N Players” section near the end of the page.


All 4N+1 combinations have directed schedules, although the only solution(s) for 9 players are not cyclical.


Directed Solutions for 5 players.

The single whist tournament solution (shown earlier) can generate 2 directed cyclical solutions.

Table     North  South   vs.  East  West
  1         2      3            4     1
      and
Table     North  South   vs.  East  West
  1         2      3            1     4

   For this example, the second schedule is merely a mirror image of the first schedule. Both solutions allow each player to play with each other player as a left opponent once, as a partner once, and as a right opponent once.

   As in the regular cyclic solutions for 4N+1 players, the person at position “0” sits out the current round. On subsequent rounds each player advances to the next position just like the regular 4N+1 solutions.


Directed Solutions for 9 players

   Earlier we showed that there are no cyclical whist tournament schedules for 9 players. However the non-cyclical example used earlier for 9 players has directed characteristics, and will cause each player to have each other player: 
1)  as a left opponent once
2)  as a partner once
3)  as a right opponent once.


         Sits           Table 1                     Table 2
Round    Out     North South   East West     North South   East West
  1       A        B  &  C  vs  D  &  G        E  &  I  vs  F  &  H
  2       B        C  &  A  vs  E  &  H        F  &  G  vs  D  &  I
  3       C        A  &  B  vs  F  &  I        D  &  H  vs  E  &  G
  4       D        E  &  F  vs  G  &  A        H  &  C  vs  I  &  B
  5       E        F  &  D  vs  H  &  B        I  &  A  vs  G  &  C
  6       F        D  &  E  vs  I  &  C        G  &  B  vs  H  &  A
  7       G        H  &  I  vs  A  &  D        B  &  F  vs  C  &  E
  8       H        I  &  G  vs  B  &  E        C  &  D  vs  A  &  F
  9       I        G  &  H  vs  C  &  F        A  &  E  vs  B  &  D

Note: In this or any other directed solution, you can transform one solution into its mirror image solution by holding the north/south player positions constant and swapping the player positions in all the east/west pairs.


Directed Solutions for 13 players

   Of the 9 general whist tournament schedules for 13 players, one of them can be used to generate 8 directed solutions such that each player has each other player as a left opponent once, as a partner once, and as a right opponent once. Note that the 8 solutions below are all formed by permutations of the east/west players.

Sol.            Table 1                    Table 2                   Table 3
Nbr.   North South   East West    North South   East West   North South   East West
 1       6     7       4    9       12     1      5    8      11     2     10    3
 2       6     7       4    9       12     1      5    8      11     2      3   10
 3       6     7       4    9       12     1      8    5      11     2      3   10
 4       6     7       4    9       12     1      8    5      11     2     10    3
 5       6     7       9    4       12     1      5    8      11     2     10    3
 6       6     7       9    4       12     1      5    8      11     2      3   10
 7       6     7       9    4       12     1      8    5      11     2      3   10
 8       6     7       9    4       12     1      8    5      11     2     10    3

   For each solution, the player who is at position “0” sits out the round. As in all cyclical solutions, the players initially start in any random order. Thereafter, on each successive round:
The player who was at position “0” moves to position “1”.
The player who was at position “1” moves to position “2”.
Etc.
The player who was at position “11” moves to position “12”.
The player who was at position “12” moves to position “0”.


Directed Solutions for 17 players

   Of the 179 general whist tournament schedules for 17 players, 83 of them can be used to generate 208 directed solutions such that each player has each other player as a left opponent once, as a partner once, and as a right opponent once. Almost all unique directed solutions will have another single mirror solution. (These mirror solutions are included in the directed solution counts.) A few other patterns derived from a general solution will have additional solutions due to east/west permutations.

The table below shows one of these directed solutions.

Table    North  South    East  West
  1        14    15        2     4
  2         5     8       13     7
  3        12    16        9     1
  4         6    11       10     3

The starting positions for all 208 cyclical Directed Bridge/Whist Tournament Schedules for 17 players can be seen here.
http://www.durangobill.com/BridgePics/BrDirWh17data.txt


Directed Solutions for 21 players

   Of the 3,900 general whist tournament schedules for 21 players, 504 of them can be used to generate 1,152 directed solutions such that each player has each other player as a left opponent once, as a partner once, and as a right opponent once.

The table below shows one of these directed solutions.

Table    North  South    East  West
  1        14    15        2     8
  2         5     7        9     4
  3        16    19       11     1
  4        13    17       12     3
  5        20     6       10    18

The starting positions for all 1,152 cyclical Directed Bridge/Whist Tournament Schedules for 21 players can be seen here.
http://www.durangobill.com/BridgePics/BrDirWh21data.txt


Directed Solutions for 25 players

  Of the 215,175 general whist tournament schedules for 25 players, 17,875 of them can be used to generate 53,400 directed solutions such that each player has each other player as a left opponent once, as a partner once, and as a right opponent once.

The table below shows one of these directed solutions.

Table    North  South    East  West
  1        17    18       19    22
  2        21    23        5     9
  3         6    11       13     1
  4        10    16       24     7
  5         8    15        2    12
  6        20     4        3    14

The starting positions for the first 1,000 cyclical Directed Bridge/Whist Tournament Schedules for 25 players can be seen here.
http://www.durangobill.com/BridgePics/BrDirWh25data.txt


Directed Solutions for 29 players

   Of the 21,500,927 general whist tournament schedules for 29 players, 904,751 of them can be used to generate 2,073,024 directed solutions such that each player has each other player as a left opponent once, as a partner once, and as a right opponent once.

The table below shows one of these directed solutions.

Table    North  South    East  West
  1        21    22        9    12
  2        25    27       19    10
  3        20    24       23    28
  4         7    13       14     2
  5         4    11       18     8
  6        26     5        3    16
  7         6    17        1    15

The starting positions for the first 1,000 cyclical Directed Bridge/Whist Tournament Schedules for 29 players can be seen here.
http://www.durangobill.com/BridgePics/BrDirWh29data.txt


A Directed Solution for 33 players

Table    North  South    East  West
  1        28    29        9    13
  2        24    26       16     2
  3         7    10        4    14
  4        27    32       25    31
  5         5    12       21    30
  6        15    23       18     3
  7        11    22        1    17
  8         8    20       19     6

The starting positions for the first 1,000 cyclical Directed Bridge/Whist Tournament Schedules for 33 players can be seen here.
http://www.durangobill.com/BridgePics/BrDirWh33data.txt


A Directed Solution for 37 players

Table    North  South    East  West
  1        29    30       34    36
  2        28    31        6    21
  3        10    14       11    23
  4         7    12       26    32
  5         9    16        3    20
  6        27    35        1    19
  7        33     5       25    15
  8        13    24        8    22
  9         4    17       18     2

The starting positions for the first 1,000 cyclical Directed Bridge/Whist Tournament Schedules for 37 players can be seen here.
http://www.durangobill.com/BridgePics/BrDirWh37data.txt


A Directed Solution for 41 players

Table    North  South    East  West
  1        13    14        3    22
  2        31    33       16    10
  3        32    35       39    27
  4        34    38       23     6
  5         7    12       11    25
  6        29    36       17     9
  7        28    37       40    30
  8        15    26        1    21
  9         5    18        8    24
 10         4    19       20     2

The starting positions for the first 500 cyclical Directed Bridge/Whist Tournament Schedules for 41 players can be seen here.
http://www.durangobill.com/BridgePics/BrDirWh41data.txt


A Directed Solution for 45 players

Table    North  South    East  West
  1        38    39        7    19
  2        13    15       34    42
  3        33    36       30    35
  4        37    41       28    14
  5        12    18        8    26
  6        10    17        5    20
  7        31    40        3    24
  8        44     9       32    43
  9        16    29        1    23
 10        11    27       22     2
 11         4    21        6    25

The starting positions for the first 100 cyclical Directed Bridge/Whist Tournament Schedules for 45 players can be seen here.
http://www.durangobill.com/BridgePics/BrDirWh45data.txt


A Directed Solution for 49 players

Table    North  South    East  West
  1         9    10       38    42
  2        15    17       39    47
  3        41    44        4    23
  4        13    18       26     3
  5        34    40       29    11
  6        12    19        5    22
  7        37    46       45    35
  8        32    43       36    48
  9        20    33        7    21
 10        16    31       25     1
 11        14    30        8    28
 12         6    27        2    24


A Directed Solution for 53 players

Table    North  South    East  West
  1        38    39       10    22
  2        15    17        6    29
  3        44    47       52     9
  4        41    45       18    13
  5        40    46       37    48
  6        43    50        8    30
  7        12    20       19    34
  8        42    51       27     1
  9        36    49       26     2
 10        21    35       25     4
 11         7    23        3    28
 12        16    33       14    32
 13         5    24       31    11


A Directed Solution for 57 players

Table    North  South    East  West
  1        41    42       19    36
  2        49    51       18    15
  3        13    17       30     3
  4        48    53       21    37
  5        40    46       56    44
  6        43    50       26     5
  7        47    55       35    16
  8        45    54       52    39
  9        12    22       27     4
 10         9    20        1    29
 11        10    24       23    38
 12         7    25       34    14
 13        11    33        8    32
 14         6    31       28     2


A Directed Solution for 61 players

Table    North  South    East  West
  1        30    31       29    32
  2        28    33       25    36
  3        27    34       23    38
  4        26    35        9    52
  5        24    37        6    55
  6        22    39        1    60
  7        21    40       12    49
  8        20    41        7    54
  9        19    42        5    56
 10        18    43       11    50
 11        17    44        2    59
 12        16    45        4    57
 13        15    46       10    51
 14        14    47        8    53
 15        13    48        3    58





   Earlier, we mentioned that there are no cyclical directed whist schedule solutions for 4N players. (4, 8, 12, 16, 20, etc.) However, if you are organizing a tournament and want to even out the skills of player combinations as much as possible, then the following schedules will minimize the number of times any player will have some other player as a left (or right) opponent more than once.

   The computer program that finds the best possible “(Almost) Directed Solution” for 4N players, uses the following algorithm.
 
  For each regular “4N” Whist Schedule              //  Sequentially process all of them
    For each permutation of the east/west players   //  There are 2^NbrTables of these
      Count the number of times a player has some
          other player as a left (or right) opponent
          more than once. This count becomes the
          “penalty” for this solution.
      Count the number of times each penalty occurs – especially the smallest penalty
    Repeat loop for all east/west permutations for this solution
  Repeat loop for all regular 4N Whist Schedules
  Output the best (smallest penalty) “(Almost) Directed Solution” and other relevant data

   In the best possible solution for 8 players (2 tables), each player will have 2 other players as left opponents twice. (Same for right opponents.) In all other solutions (4, 12, 16, 20, etc. players), each player will have some other player who will repeat as a left opponent just once. (Also some other player will repeat as a right opponent once.)  The only exception to the rule will be the player who remains at position “0”. This player will have every other player as a left opponent once, and as a right opponent once.

   Finally, the totals for the “almost” solutions contain many duplicates. The number of unique solutions will be only half (or less) of the given totals.

Player rotation sequences are similar to the ordinary whist tournament schedules for 4N players.


An “Almost” Directed Solution for 4 Players

   There is only one regular whist tournament schedule for 4 players. This solution has two possible east/west permutations, and the schedule shown below has the minimum “penalty” of these two solutions.

Table    North  South    East  West
  1         1      2       3     0


An “Almost” Directed Solution for 8 Players

   There are 6 regular whist tournament schedules for 8 players. Each of these has 4 possible east/west permutations. This yields 24 possible solutions such that the north, south, east, and west positions are defined. All 24 have the same minimum penalty. One of these solutions is shown below.

Table    North  South    East  West
  1        2      3        4     6
  2        5      1        7     0


An “Almost” Directed Solution for 12 Players

   There are 20 regular whist tournament schedules for 12 players. Each of these has 8 possible east/west permutations. This yields 160 possible solutions such that the north, south, east, and west positions are defined. Of these 160 possible solutions, there are 20 that share the minimum penalty. One of these is shown below.

Table    North  South    East  West
  1        8      9        4     6
  2        2      5       10     3
  3        7      1       11     0


An “Almost” Directed Solution for 16 Players

   There are 128 regular whist tournament schedules for 16 players. Each of these has 16 possible east/west  permutations. This yields 2,048 possible solutions such that the north, south, east, and west positions are defined. Of these 2,048 possible solutions, there are 48 that share the minimum penalty. One of these is shown below.

Table    North  South    East  West
  1        6      7        1     5
  2       10     12        9     2
  3       11     14        3     8
  4       13      4       15     0


An “Almost” Directed Solution for 20 Players

   There are 1,710 regular whist tournament schedules for 20 players. Each of these has 32 possible east/west permutations. This yields 54,720 possible solutions such that the north, south, east, and west positions are defined. Of these 54,720 possible solutions, there are 504 that share the minimum penalty. One of these is shown below.

Table    North  South    East  West
  1       17     18        9    15
  2       14     16       12     7
  3        2      5       10     1
  4        4      8        3    11
  5        6     13       19     0


An “Almost” Directed Solution for 24 Players

   There are 81,576 regular whist tournament schedules for 24 players. Each of these has 64 possible east/west permutations. This yields 5,220,864 possible solutions such that the north, south, east, and west positions are defined. Of these 5,220,864 possible solutions, there are 18,216 that share the minimum penalty. One of these is shown below.

Table    North  South    East  West
  1       17     18        3    13
  2       20     22        9     6
  3       15     19        8    16
  4        5     10        2    11
  5       21      4        0    23
  6        7     14       12     1


An “Almost” Directed Solution for 28 Players

   There are 7,910,127 regular whist tournament schedules for 28 players. Each of these has 128 possible east/west permutations. This yields 1,012,496,256 possible solutions such that the north, south, east, and west positions are defined. Of these 1,012,496,256 possible solutions, there are 918,252 that share the minimum penalty. One of these is shown below.

Table    North  South    East  West
  1        9     10       25     5
  2       21     23       12     6
  3        8     11       15     3
  4       16     20       17     7
  5       19     24       18    26
  6       22      4       14     1
  7        2     13       27     0


An “Almost” Directed Solution for 32 Players

Table    North  South    East  West
  1       11     12       13    23
  2        7      9       30    25
  3       24     27       29    20
  4       22     26       17     1
  5        4     10       21    28
  6        6     14       18     5
  7        8     19       16     2
  8        3     15       31     0


An “Almost” Directed Solution for 36 Players

Table    North  South    East  West
  1       26     27       10    12
  2       29     32        2    18
  3        9     13       16     4
  4        6     11       31     7
  5       28     34        0    35
  6       23     30        1    19
  7       14     22       20     5
  8       24     33       21     8
  9       15     25        3    17


An “Almost” Directed Solution for 40 Players

Table    North  South    East  West
  1       35     36        5    22
  2       32     34       37    30
  3        9     12       19     3
  4       27     31       17     7
  5       28     33       16    10
  6        6     14       25    13
  7       29     38        1    21
  8       15     26        2    20
  9       11     24       23     8
 10        4     18        0    39


An “Almost” Directed Solution for 44 Players

Table    North  South    East  West
  1       32     33        8    25
  2       34     36        2    22
  3       12     15        9    41
  4       35     39       31    40
  5       37     42        4    20
  6       10     16       23     1
  7        7     14       27    13
  8       30     38       11    26
  9       18     28        0    43
 10       17     29        6    19
 11        3     21        5    24


An “Almost” Directed Solution for 48 Players

Table    North  South    East  West
  1       39     40       32    41
  2       15     17       37    33
  3        9     12        0    47
  4       14     19       27     8
  5       38     44        6    21
  6       35     42       30    16
  7       10     18        7    20
  8       36     46       23     3
  9       34     45       13    29
 10       31     43        2    24
 11       11     28       25     1
 12        4     22       26     5


An “Almost” Directed Solution for 52 Players

Table    North  South    East  West
  1       14     15       11    30
  2       39     41       10    50
  3       17     20        9    21
  4       38     42       24     4
  5       44     49       47    34
  6       12     18       37    46
  7       36     43       31    13
  8       40     48       28     2
  9       35     45       29     8
 10       19     33       25     1
 11        7     22        0    51
 12       16     32        6    23
 13        5     27        3    26


An “Almost” Directed Solution for 56 Players

Table    North  South    East  West
  1       14     15       21    36
  2       18     20       37    50
  3       43     46        5    30
  4       49     53        9    23
  5       12     17        8    31
  6       38     44       54    45
  7       41     48       13    33
  8       39     47       16    34
  9       42     52       40    51
 10       10     22        2    28
 11       19     35        7    24
 12        6     25        3    27
 13       11     32       29     1
 14        4     26        0    55


An “Almost” Directed Solution for 60 Players

Table    North  South    East  West
  1       57     58       45    51
  2       18     20       16    36
  3       47     50       28     2
  4       44     48       38    21
  5       12     17       27     4
  6       42     49       11    33
  7       15     23       40    53
  8       13     22       10    24
  9       46     56       37    19
 10       41     52       26     7
 11       43     55       35    14
 12       39     54        0    59
 13        9     25        8    32
 14        6     31       30     3
 15        1     29       34     5




   In the ““Conveyor Belt Algorithm” for Simple Partnerships” section we asked the question:
Is there more than one way to schedule a Round Robin tournament such that each player plays against each other player once (or each team plays against each other team once)? The answer is “Yes”.

   As to how many ways this can be done for “N” pairs (alternately “2N” players), we have already given some answers in the “Qualifying Nbr Teams via Program” columns in the tables. These numbers can also be found in the “The On-Line Encyclopedia of Integer Sequences” at http://oeis.org/A006204 . “Number of starters in cyclic group of order 2n+1”

  These “Starters” are basically synonymous with the number of cyclic configurations that exist such that each player (or team) can play against each other player (or team) exactly once in a Round Robin tournament. The number of different cyclic configurations for 4 to 38 players is shown in the table below. (The “Solutions Files” have up to 1,000 initial configurations for larger groups.)

   The results shown through 18 pairs (36 players) were found by other researchers, but all values shown below have been independently confirmed by the author. The results for 19 pairs (38 players) were found by the author. Computations for the last entry took a little under 2 weeks on my personal computer - an Intel i7-970 six-core 3.2 GHz machine. (Multiple copies of the program would run in parallel for 24 hours a day. If the engineers at Intel ever want an independent test involving “putting the screws” to any new version of their CPUs, please contact me.)

   Results for 2 to 18 pairs were initially found by a “depth first” algorithm and subsequently confirmed by a couple of variations of “breadth first” algorithms. The 28,311,543,893,885 combinations for 38 players used a modified “breadth first” approach. A pure “breadth first” algorithm would find the results in less than a day, but would require about 200 GB of RAM to do it in a single program run.


  Number     Number         Number  of      Nbr. Of Config.       Solutions
of Pairs  of Players     Configurations      (No commas)           Files
    2           4                     1                  1     StarterData02
    3           6                     1                  1     StarterData03
    4           8                     3                  3     StarterData04
    5          10                     9                  9     StarterData05
    6          12                    25                 25     StarterData06
    7          14                   133                133     StarterData07
    8          16                   631                631     StarterData08
    9          18                 3,857               3857     StarterData09
   10          20                25,905              25905     StarterData10
   11          22               188,181             188181     StarterData11
   12          24             1,515,283            1515283     StarterData12
   13          26            13,376,125           13376125     StarterData13
   14          28           128,102,625          128102625     StarterData14
   15          30         1,317,606,101         1317606101     StarterData15
   16          32        14,534,145,947        14534145947     StarterData16
   17          34       170,922,533,545       170922533545     StarterData17
   18          36     2,138,089,212,789      2138089212789     StarterData18
   19          38    28,311,543,893,885     28311543893885     StarterData19
   20          40                     ?                  ?     StarterData20
   21          42                     ?                  ?     StarterData21
   22          44                     ?                  ?     StarterData22
   23          46                     ?                  ?     StarterData23
   24          48                     ?                  ?     StarterData24
   25          50                     ?                  ?     StarterData25

   The computer program results for 19 pairs (38 players) finished on June 26, 2012. Minor modifications to the computer program were made, and a 2nd run was made to see if there were any transcribing errors and/or other differences as compared to the initial results. The second program run finished on July 10, 2012 and exactly duplicated the earlier results.

   The “Number of Configurations” columns show how many different “initial cyclic configurations” are possible such that each player plays against each other player once in a Round Robin type tournament.

   If you click on any of the “Solutions Files”, you can see up to 1,000 solutions for the particular Number of Pairs/Players. Each of the solutions can be used as a starting configuration for a Round Robin tournament where each player plays against each other player once. In each solution, players can start at random positions. On each subsequent round, each player moves to the next highest position, except that whoever was at position “0” stays there and the player who was at the last position (rightmost column in the files) cycles back to position 1. After “Number of Players less one” rounds, each player will have played against each other player once.

Note: The original computation time for the “2,138,089,212,789”
“took about 23 months of CPU time on an HP CP4000 BL ProLiant supercluster”
(“Open” the file at: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.168.2315&rep=rep1&type=pdf )

Would anyone like to compare algorithms? (My PC figures that someone has to show the “supercluster” who’s boss.)



Examples:

   If you have 8 players (matched into 3 active pairs + 1 static pair), there are three possible cyclic configurations.

Pair Nbr.    Configuration 1    Configuration 2    Configuration 3    Span Distance
    1            2 vs. 5            5 vs. 1            6 vs. 2              3
    2            6 vs. 1            4 vs. 6            1 vs. 3              2
    3            3 vs. 4            2 vs. 3            4 vs. 5              1
    4            0 vs. 7            0 vs. 7            0 vs. 7              0

   For any one of the 3 possible configurations, the 8 players would start in random positions. On each subsequent round, the player who initially starts at position “0” stays there. The other 7 players advance one position on each round except whoever was at position “7” cycles back to position “1”. After 7 rounds of play, each of the 8 players will have played against each of the other 7 players exactly once.


   If you have 10 players (matched into 4 active pairs + 1 static pair), there are nine possible cyclic configurations.

Pair  Config   Config   Config   Config   Config   Config   Config   Config   Config  Span
Nbr.     1        2        3        4        5        6        7        8        9    Dist
  1   1 vs 5   1 vs 5   2 vs 6   3 vs 7   4 vs 8   4 vs 8   6 vs 1   7 vs 2   8 vs 3    4
  2   3 vs 6   4 vs 7   1 vs 4   5 vs 8   2 vs 5   3 vs 6   8 vs 2   3 vs 6   7 vs 1    3
  3   2 vs 4   6 vs 8   3 vs 5   4 vs 6   1 vs 3   5 vs 7   5 vs 7   8 vs 1   2 vs 4    2
  4   7 vs 8   2 vs 3   7 vs 8   1 vs 2   6 vs 7   1 vs 2   3 vs 4   4 vs 5   5 vs 6    1
  5   0 vs 9   0 vs 9   0 vs 9   0 vs 9   0 vs 9   0 vs 9   0 vs 9   0 vs 9   0 vs 9    0

   Again, for any one of the 9 possible configurations, the 10 players would start in random positions. On each subsequent round, the player who initially starts at position “0” stays there. The other 9 players advance one position on each round except whoever was at position “9” cycles back to position “1”. After 9 rounds of play, each of the 10 players will have played against each of the other 9 players exactly once.

   The symmetry in the above solutions is of interest. If we look at the solutions for 10 players, we note that “Config 6” is the symmetrical compliment of “Config 1”. If you add the position number for any player position in “Config 1” to its symmetrical compliment in “Config 6”, the result is always “9”. Similarly, solutions 2 & 5, 3 & 4, and 7 & 9 are symmetrical pairs. Config 8 is a “Patterned Solution”, and thus it is its own symmetrical compliment. (The opponent pairs all sum to 9.)

   Similar symmetry exists for all other orders. (Number of players) All solutions will have a symmetrical compliment except there will be a single “Patterned Solution/Starter” for each order. Note that this single “Patterned Starter” will cause the solution count for each order to be an “odd number”.

  The table at http://www.durangobill.com/BridgePics/StartersData.txt shows the number of solutions (including subtotals) for the pair groups up to 19 pairs. (Details for the above Numbers of Starters table) For example, if we use the “10 players” results, there are:


The symmetry that shows up is of considerable help as it cuts the computer run time by a factor of 2.

   Note: The solid “chord” lines in all of the preceding “Span Diagrams” are all solutions to the Player vs. Player scheduling problem. In turn, any solution to the Player vs. Player problem can be plotted as a “Span Diagram”. However, an arbitrary “solid chord line” solution for the Player vs. Player problem may not lead to a “Whist Schedule” solution.





   Any of the above solutions can be easily adapted for a brother/spouse avoidance schedule. In a brother/spouse avoidance schedule, a player has all players except his brother/spouse as a partner once (whist tournament) or as an opponent once (round robin tournaments for pairs).

   Instead of initially seating players randomly, players are seated for an initial “pseudo round” such that all brother/spouse pairs are matched with their brother/spouse. Since all regular solutions pair each person with each other person exactly once, this “pseudo round” eliminates all brother/spouse matchups. Then all players (except the person at “0”) advance one position as per the usual cycles, and start playing real rounds.

   The total number of real rounds will be decreased by one from what would happen if you did not add the brother/spouse avoidance constraint. This won’t make any difference for pairs combinations; but for whist schedules, there will be a few players who will be an opponent just once instead of twice.






   Permission is granted to anyone who may wish to use information on this web page for any not-for-profit use provided acknowledgement is made to the author (Bill Butler) and a reference is included to this web page. (http://www.durangobill.com/BridgeCyclicSolutions.html)


Bill Butler


Return to the main Bridge page

Return to Durango Bill’s home page

Web page generated via Sea Monkey's Composer HTML editor
within  a Linux Cinnamon Mint 18 operating system.
(Goodbye Microsoft)