
Durango Bill's
The “Integer Brick” Problem
(The Euler Brick Problem)
Is it possible to construct a rectangular solid such that the dimensions of all sides
and all diagonals including the interior diagonal through the center are integers?
This
is an unsolved problem as no one has found an example, but
no one has proved that a solution can’t exist. If a
solution exists, its “odd” side is greater than 3.0
trillion (3.0E+12) - no restrictions on the other
dimensions.
The search has been terminated at 3.0 trillion as it is assumed that any additional search will still not find the “Jackalope”. http://en.wikipedia.org/wiki/Jackalope
The search has been terminated at 3.0 trillion as it is assumed that any additional search will still not find the “Jackalope”. http://en.wikipedia.org/wiki/Jackalope
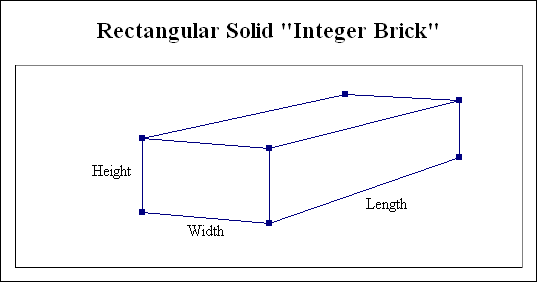
The diagram above
illustrates a rectangular solid (a “brick”). The dimensions of
the rectangular solid (the “brick”) are defined by its length,
width, and height. Since the six sides of a rectangular solid
are all rectangles, the size of any diagonal contained in any
of these sides can be calculated using the Pythagorean
Theorem.
The Pythagorean Theorem states that the relationship between the two sides of a right triangle and its sloping third side (the hypotenuse) will obey the following equation.
(Side 1)2 + (Side 2)2 = Hypotenuse2
Where (Side 1)2 means: (Side 1) times (Side 1)
Alternately this equation can be expressed as:
Hypotenuse = Sqrt[ (Side 1)2 + (Side 2)2]
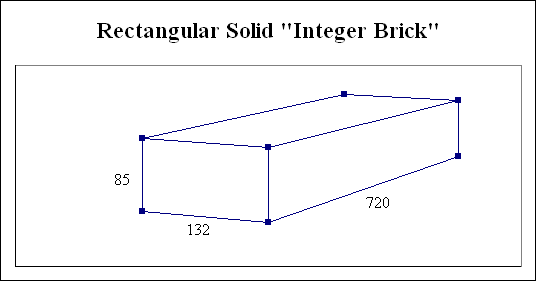
The following diagram illustrates how the Pythagorean Theorem can be used to calculate the external diagonals of a rectangular solid (our brick).
The Pythagorean Theorem states that the relationship between the two sides of a right triangle and its sloping third side (the hypotenuse) will obey the following equation.
(Side 1)2 + (Side 2)2 = Hypotenuse2
Where (Side 1)2 means: (Side 1) times (Side 1)
Alternately this equation can be expressed as:
Hypotenuse = Sqrt[ (Side 1)2 + (Side 2)2]
The following diagram illustrates how the Pythagorean Theorem can be used to calculate the external diagonals of a rectangular solid (our brick).

In the above diagram, we note
the following dimensions:
Length = 720
Width = 132
Height = 85
These three dimensions are all integers. So far, there are no problems finding our “all integers” solution.
We can use the Pythagorean Theorem to calculate the external diagonals involved since these diagonals are all equivalent to the hypotenuse of a right triangle.
For the outside surface at the left end we have:
Hypotenuse (the diagonal) = Sqrt(Heigth2 + Width2)
Using our example gives:
Diagonal = Sqrt(852 + 1322)
= 157
A similar calculation for the front, right surface yields:
Hypotenuse (the diagonal) = Sqrt(Height2 + Length2)
Diagonal = Sqrt( 852 + 7202)
= 725
And finally we can find the diagonal across the top surface:
Hypotenuse (the diagonal) = Sqrt(Width2 + Length2)
Diagonal = Sqrt(1322 + 7202)
= 732
So far, we have integer length-width-height dimensions for the brick and all of its external diagonals. For most brick dimensions the external diagonals will not be integers. However, an infinite number of “bricks” exist that do have integer external diagonals. Some examples include:
Height Width Length
85 132 720
117 44 240
231 160 792
275 240 252
351 132 720
693 140 480
825 720 756
The above table includes “primitive” solutions (one side is odd) and “odd” multiples of primitive solutions where all 3 sides are < 1000.
As an exercise in using the Pythagorean Theorem, you may want to use these combinations to verify that they all have integer external diagonals.
The internal diagonal that runs from any given corner through the center of the rectangular solid and terminates at the far corner can also be calculated using the Pythagorean Theorem. One combination for the two sides to this triangle would be “height” and “top-surface diagonal”. In our example we would use the height of 85 and the top surface diagonal which we previously calculated and found to be 732. (Note: Other dimension/diagonal combinations are also valid. Alternately, you could calculate the size of the center diagonal using:
Center Diagonal = Sqrt( Height2 + Width2 + Length2)
The calculation here would be:
Hypotenuse (center diagonal) = Sqrt(Height2 + Top-surface-diagonal2)
Center Diagonal = Sqrt (852 + 7322)
Note that Sqrt(852 + 1322 + 7202) will produce the same result.
Unfortunately this ends up equaling 736.91858+ which is not an integer. It starts getting worse as none of the other integer dimension examples (shown above) work either. In fact there is no known combination of dimensions that work. On the other hand, no one has proved that there are no solution combinations. Thus it is an unsolved problem in mathematics.
If you could find a dimension combination such that all diagonals are integers, including the central diagonal, the world might reward you with fame, gifts, money, etc. for solving the unsolved problem. (This might be a “slight exaggeration”, but at least your name would be recorded as “the solver”). In this pursuit you might try writing a computer program to try a large number of combinations to see if a solution could be found. A possible algorithm might be:
For (Length equals 1 to billions - or more) // Try a bunch of possible lengths
For (Width equals 1 to billions – or more) // Same for width
For (Height equals 1 to billions, etc) // Hey, just do more of the same
Do all the length2, height2, width2, Sqrt() calculations
reviewed previously to see if anything works.
Repeat this loop for a whole bunch of possible “heights”
Repeat this loop for a whole bunch of possible “widths”
Repeat for a whole bunch of possible “lengths”
Technically, if a solution exists, this algorithm would find it. In reality, the number of calculations required is mind boggling. You and the universe will die of old age before your search gets very far.
The search speed of the above algorithm can be substantially improved by taking the first test for an integer diagonal from inside the innermost loop and placing it inside the second loop. At 1.0E12 (and above) this improvement will increase the running speed of a computer program by a factor of billions. The result might look like the following:
// Note: Length > Width > Height
// For all possible lengths
for (Length = StartLength; Length; Length += 1.0) { // Length will increment forever
for (Width = Length - 1.0; Width > 1.0; Width -= 1.0) { // For all possible widths down to 2
Diagonal = hypot(Length, Width); // Get the hypotenuse for side 1
if (Diagonal != floord(Diagonal)) // If it's not an integer,
continue; // then skip the inner calcs
// Else, for all possible heights
for (Height = Width - 1.0; Height > 0.0; Height -= 1.0) { // down to 1
Diagonal = hypot(Length, Height); // Get the hypotenuse for side 2
if (Diagonal != floord(Diagonal)) // If it's not an integer, then
continue; // skip to the end of the loop.
Diagonal = hypot(Width, Height); // Get the hypotenuse for side 3
if (Diagonal != floord(Diagonal)) // If it's not an integer, then
continue; // skip to the end of the loop.
// If to here, then found an
// external solution.
SolCount++;
printf("\nExternal solution Nbr %'d\n", SolCount);
printf("Length = %'.0f Width = %'.0f Height = %'.0f\n",
Length, Width, Height);
// Check for an internal solution
Diagonal = hypot(Diagonal, Length); // Get the internal diagonal
if (Diagonal == floord(Diagonal)) // If it's an integer,
puts("The above is a complete solution");
} // End of "Height" loop
} // End of "Width" loop
} // End of "Length" loop
While the above (part of an actual computer program) improves upon the original algorithm by a factor of billions (at 1.0E12 and above), the algorithm given below is billions of times faster yet. (At 1.0E12 and above as measured by time trials.)
If you are going to run a serious search, you should use the best algorithm that is available.
Since you are going to let a computer program try to find a solution, you should at least give it a good set of rules to work with. You still might not find a solution, but you can greatly increase the search area for the dimensions of “the brick”.
In the inefficient algorithms given above, we just tried “a whole bunch of numbers” and then applied the calculations of the Pythagorean Theorem to see if the diagonals were integers. It is much faster to use algebraic expressions derived from the Pythagorean Theorem to directly generate right triangles where the hypotenuse is also an integer.
First, we note that all the “brick” examples given earlier had one dimension that was “odd”, while the other two dimensions were “even”. If a solution exists for the integer brick problem, then either this solution is a “primitive” solution, or it is a multiple of a primitive solution. If a primitive solution exists, exactly one of its dimensions will be “odd” while the other two dimensions will be “even”. (If all three dimensions were even, then everything could be repeatedly divided by 2 until one of the dimensions became odd. There can’t be two sides that are “odd” as the “Y” side of an integer Pythagorean Triangle must be even. See calculations below.)
If we represent the sides of a right triangle by the variables “X”, “Y”, and “Z” (where “Z” is the hypotenuse), then right, integer triangles can be generated using the following equations:
For example, if we let P = 2, Q = 1, and K = 1, then we get X = 3, Y = 4, and Z = 5. This is the smallest possible integer right triangle.
We note that the “X” term above has three components: (P-Q), (P+Q), and K. If we are going to generate “odd” numbers for our trial bricks, then each of these components must be odd. For example, if we want to generate a trial brick where the odd side is equal to 85, then the 85 is separated into three components whose product equals 85. Here, the only two possibilities are 1 times 5 times 17 and 1 times 1 times 85. (These triplets can be in any order.) We will use these triplets to solve for “P”, “Q”, and “K”. In turn, we will use the results to generate the 85, 132, 720 example given earlier that “almost” solves the integer brick problem.
In the multiplication of 1 x 5 x 17 = 85, the 1, 5, and 17 factors can be in an order. However, the terms (P-Q)(P+Q)K require (P+Q) to be larger than (P-Q). Thus, for our multiplication, we only use permutations where the second term is larger than the first. We now have:
1 x 5 x 17 = 85
1 x 17 x 5 = 85
5 x 17 x 1 = 85
Each of these can be solved to get a “P”, “Q”, “K” triplet
If we let (P-Q) = 1 and (P+Q) = 5, then we get P = 3, Q = 2, and K = 17
Substituting these in Y = 2PQK yields Y = 204 (In practice, this result won’t be useful)
If we let (P-Q) = 1 and (P+Q) = 17, then we get P = 9, Q = 8, and K = 5
Substituting these in Y = 2PQK yields Y = 720 (One of the sides in our brick)
Finally, if we let (P-Q) = 5 and (P+Q) = 17, then we get P = 11 , Q = 6, and K = 1
Substituting these in Y = 2PQK yields Y = 132 (The other side that we used in the brick)
The only other valid multiplication is:
1 x 85 x 1 = 85
If we let (P-Q) = 1 and (P+Q) = 85, then we get P = 43, Q = 42, and K = 1
Substituting these in Y = 2PQK yields Y = 3612.
Thus we have found the four right triangles that can have one side equal to 85. The other side can equal 132, 204, 720, or 3612. (These are the only four. There are no others.)
These four results are then tried in various combinations for trial sides of the integer brick. You can reduce the trial combinations a great deal further by observing that if a solution exists, the “top-surface” diagonal would be one of the members of the above trial list.
In the above example, there are only 4 divisors of 85 (1, 5, 17, and 85). For other odd “X” sides, there may be many possible triplets. (e.g. If the odd number is a product of many small odd prime numbers.) Our more efficient algorithm thus becomes:
For “odd side” equals 3, 5, 7, etc.
Generate all possible triplets that can be multiplied to produce the odd number
For each valid permutation, solve for P, Q, K and the second side of a right triangle
Make a list of all of these trial “Side 2’s”
Search the list to see if any combination yields a solution
Repeat the above for the next odd number.
Finally, we have not mentioned an efficient way to find the “triplet” trial divisors. You could of course try dividing the “odd side” by 3, 5, 7, etc. up to Sqrt(odd number). This is not efficient.
A much faster way of finding trial divisors for the “triplets” can be found using a “sieve” algorithm. In the table below, note where the “1’s” show up.
Trial < - - - - Trial “Odd Numbers” - - - - >
Divs. 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 . . . 85 . . .
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
3 1 0 0 1 0 0 1 0 0 1 0 0 1 0 0 1 0 0
5 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 1
7 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0
9 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0
11 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0
13 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0
15 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0
17 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1
.
.
85 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
Etc.
The top row lists the trial odd numbers that will be used for the odd side of the brick. The left edge lists all odd numbers which potentially might be evenly divisible into the trial odd number.
All possible trial numbers are divisible by 1. We know that 3 can be divided by 3. Then we simply go three columns to the right of this number to find another trial odd number that is also divisible by 3. We can continue going right 3 columns at a time as far as needed.
A similar process works for Trial Divisor = 5. We just mark a “1” in every 5th column. The process can be extended for as many rows as needed. If you use this “sieve” method to find trial divisors, all you have to do is start a list for each column. Then process each row by adding a new divisor to the appropriate list each time a “1” would be encountered. (For computer science students, think “Link List”). Periodically, a large block of the table can be generated which will generate lists for large numbers of trial “Odd Numbers”.
In the program, a block for these divisor lists is 100,000 columns wide. (Trial “Odd Numbers” increase by 200,000 per block.) With Trial “Odd Numbers” in the 1.0E11 to 1.0E12 range, on average there are near to slightly over 6 divisors per column. Thus the program generates about (to a little over) 600,000 nodes in the divisor lists per block.
The author wrote a computer program based on the algorithm outlined above. (Actually, a couple of different versions were used.) Initially, all odd numbers out to 21 billion were tried on a Pentium 4 computer. Subsequently, a Skulltrail computer was used to extend the search out to 3.0 trillion. (3.0E+12). All versions of the program were written in “C” and used the lcc-win32 C compiler system. (http://www.cs.virginia.edu/~lcc-win32/)
It should be noted that if the odd side of a right triangle is represented by the variable “X”, then the even side can be as large as (X2 -1)/2. Thus, if the odd side is 1.0E+12, the even side can be as large as 5.0E+23. This has more digits than the precision that exists on Intel processors. Then of course these numbers have to be squared for the X2 + Y2 calculations. Thus, the computer program has to keep track of the extra precision.
No solutions were found.
The best chance of finding a possible solution would appear to occur when the “odd side” of the brick is a product of many small factors. For example, at “odd side” = 9,704,539,845 (3x3x5x7x11x13x17x19x23x29) the program generated 16,402 right triangles that shared the same common odd edge. Even with this many candidates for the other dimensions of the brick, there were no combinations that produced a solution.
The possibility exists that the computer program is faulty, and a solution actually exists somewhere in the search range. Viewers are encouraged to launch their own search efforts in case a solution actually exists.
An external solution consists of integer edges and integer external diagonals. One version of the program generated a disk file that contained all the external solutions with the 3 sides <= 1,000,000,000 with one side “odd”.
There were 4,631 of these which were subsequently read into a spreadsheet so that they could be “played with”. Click here if you would like to view/copy this list.
Various experiments were tried using Greatest Common Divisor, Mod 2 arithmetic, Mod 3 arithmetic, etc. (e.g. The product of the 3 dimensions is always divisible by 95,040.) No reliable pattern was recognized that would prevent a solution that would also include an integer internal diagonal.
The 7 external solutions with all 3 dimensions under 1,000 were given earlier. However, only 5 of these are primitive. (A primitive solution has no common divisor for the 3 edges.)
The following table shows the number of primitive external solutions where the 3 sides are no larger than the Dimension Limit.
Number of
Dimension Primitive
Limit Solutions
1,000 5
10,000 19
100,000 65
1,000,000 242
10,000,000 704
100,000,000 1,884
1,000,000,000 4,631
10,000,000,000 10,943
100,000,000,000 43,106
External solutions come in all shapes and sizes.
For example, there are long flat solutions:
X Y Z
74,745 23,085,952 186,227,160
Nearly cubical solutions:
X Y Z
110,562,771 108,192,528 109,141,700
Multiple solutions for a given height:
X Y Z
1,155 1,008 1,100
1,155 6,688 6,300
If anyone would like to view/use the “C” source code for the program, it is available here ( http://www.durangobill.com/IntBrickSourceCode.html ) It should compile “as is” using the lcc win32 “C” compiler. If you have any questions please feel free to ask. (My E-mail address is on my home page) If you publish any results that use the program (or derivatives thereof), I would appreciate an acknowledgement that I supplied the original code/algorithm.
If you compile and run the program, you will get a lot of output in the first few seconds. This will include a lot of status information. If you start the search at 0, this will also include external solutions with the odd side of the brick < 5000. However, things will quickly quiet down to just periodic status information after the first few seconds. (About as exciting as watching grass grow.)
If you find an error/bug in the program, please let me know so I can fix it and try again. (I’m pretty sure the program is OK, but there’s no 100% guarantee on these things.)
For additional information about the Euler Brick Problem please see:
Eric Weisstein’s "Perfect Cuboid" web page: http://mathworld.wolfram.com/PerfectCuboid.html
and
Fred Curtis’s "Primitive Euler Bricks" web page: http://f2.org/maths/peb.html
Return to Durango Bill's Home Page
Length = 720
Width = 132
Height = 85
These three dimensions are all integers. So far, there are no problems finding our “all integers” solution.
We can use the Pythagorean Theorem to calculate the external diagonals involved since these diagonals are all equivalent to the hypotenuse of a right triangle.
For the outside surface at the left end we have:
Hypotenuse (the diagonal) = Sqrt(Heigth2 + Width2)
Using our example gives:
Diagonal = Sqrt(852 + 1322)
= 157
A similar calculation for the front, right surface yields:
Hypotenuse (the diagonal) = Sqrt(Height2 + Length2)
Diagonal = Sqrt( 852 + 7202)
= 725
And finally we can find the diagonal across the top surface:
Hypotenuse (the diagonal) = Sqrt(Width2 + Length2)
Diagonal = Sqrt(1322 + 7202)
= 732
So far, we have integer length-width-height dimensions for the brick and all of its external diagonals. For most brick dimensions the external diagonals will not be integers. However, an infinite number of “bricks” exist that do have integer external diagonals. Some examples include:
Height Width Length
85 132 720
117 44 240
231 160 792
275 240 252
351 132 720
693 140 480
825 720 756
The above table includes “primitive” solutions (one side is odd) and “odd” multiples of primitive solutions where all 3 sides are < 1000.
As an exercise in using the Pythagorean Theorem, you may want to use these combinations to verify that they all have integer external diagonals.
The internal diagonal that runs from any given corner through the center of the rectangular solid and terminates at the far corner can also be calculated using the Pythagorean Theorem. One combination for the two sides to this triangle would be “height” and “top-surface diagonal”. In our example we would use the height of 85 and the top surface diagonal which we previously calculated and found to be 732. (Note: Other dimension/diagonal combinations are also valid. Alternately, you could calculate the size of the center diagonal using:
Center Diagonal = Sqrt( Height2 + Width2 + Length2)
The calculation here would be:
Hypotenuse (center diagonal) = Sqrt(Height2 + Top-surface-diagonal2)
Center Diagonal = Sqrt (852 + 7322)
Note that Sqrt(852 + 1322 + 7202) will produce the same result.
Unfortunately this ends up equaling 736.91858+ which is not an integer. It starts getting worse as none of the other integer dimension examples (shown above) work either. In fact there is no known combination of dimensions that work. On the other hand, no one has proved that there are no solution combinations. Thus it is an unsolved problem in mathematics.
Using a
Computer Program to try to find a Solution
If you could find a dimension combination such that all diagonals are integers, including the central diagonal, the world might reward you with fame, gifts, money, etc. for solving the unsolved problem. (This might be a “slight exaggeration”, but at least your name would be recorded as “the solver”). In this pursuit you might try writing a computer program to try a large number of combinations to see if a solution could be found. A possible algorithm might be:
For (Length equals 1 to billions - or more) // Try a bunch of possible lengths
For (Width equals 1 to billions – or more) // Same for width
For (Height equals 1 to billions, etc) // Hey, just do more of the same
Do all the length2, height2, width2, Sqrt() calculations
reviewed previously to see if anything works.
Repeat this loop for a whole bunch of possible “heights”
Repeat this loop for a whole bunch of possible “widths”
Repeat for a whole bunch of possible “lengths”
Technically, if a solution exists, this algorithm would find it. In reality, the number of calculations required is mind boggling. You and the universe will die of old age before your search gets very far.
The search speed of the above algorithm can be substantially improved by taking the first test for an integer diagonal from inside the innermost loop and placing it inside the second loop. At 1.0E12 (and above) this improvement will increase the running speed of a computer program by a factor of billions. The result might look like the following:
// Note: Length > Width > Height
// For all possible lengths
for (Length = StartLength; Length; Length += 1.0) { // Length will increment forever
for (Width = Length - 1.0; Width > 1.0; Width -= 1.0) { // For all possible widths down to 2
Diagonal = hypot(Length, Width); // Get the hypotenuse for side 1
if (Diagonal != floord(Diagonal)) // If it's not an integer,
continue; // then skip the inner calcs
// Else, for all possible heights
for (Height = Width - 1.0; Height > 0.0; Height -= 1.0) { // down to 1
Diagonal = hypot(Length, Height); // Get the hypotenuse for side 2
if (Diagonal != floord(Diagonal)) // If it's not an integer, then
continue; // skip to the end of the loop.
Diagonal = hypot(Width, Height); // Get the hypotenuse for side 3
if (Diagonal != floord(Diagonal)) // If it's not an integer, then
continue; // skip to the end of the loop.
// If to here, then found an
// external solution.
SolCount++;
printf("\nExternal solution Nbr %'d\n", SolCount);
printf("Length = %'.0f Width = %'.0f Height = %'.0f\n",
Length, Width, Height);
// Check for an internal solution
Diagonal = hypot(Diagonal, Length); // Get the internal diagonal
if (Diagonal == floord(Diagonal)) // If it's an integer,
puts("The above is a complete solution");
} // End of "Height" loop
} // End of "Width" loop
} // End of "Length" loop
While the above (part of an actual computer program) improves upon the original algorithm by a factor of billions (at 1.0E12 and above), the algorithm given below is billions of times faster yet. (At 1.0E12 and above as measured by time trials.)
If you are going to run a serious search, you should use the best algorithm that is available.
Designing
a better algorithm
Since you are going to let a computer program try to find a solution, you should at least give it a good set of rules to work with. You still might not find a solution, but you can greatly increase the search area for the dimensions of “the brick”.
In the inefficient algorithms given above, we just tried “a whole bunch of numbers” and then applied the calculations of the Pythagorean Theorem to see if the diagonals were integers. It is much faster to use algebraic expressions derived from the Pythagorean Theorem to directly generate right triangles where the hypotenuse is also an integer.
First, we note that all the “brick” examples given earlier had one dimension that was “odd”, while the other two dimensions were “even”. If a solution exists for the integer brick problem, then either this solution is a “primitive” solution, or it is a multiple of a primitive solution. If a primitive solution exists, exactly one of its dimensions will be “odd” while the other two dimensions will be “even”. (If all three dimensions were even, then everything could be repeatedly divided by 2 until one of the dimensions became odd. There can’t be two sides that are “odd” as the “Y” side of an integer Pythagorean Triangle must be even. See calculations below.)
If we represent the sides of a right triangle by the variables “X”, “Y”, and “Z” (where “Z” is the hypotenuse), then right, integer triangles can be generated using the following equations:
X = (P2 – Q2)K
(We
will
let “X” = an odd number. Alternately: X =
(P-Q)(P+Q)K)
Y = 2PQK (Since either P or Q must be even, Y is always divisible by 4)
Z = (P2 + Q2)K (We won’t use this equation in the actual computer algorithm)
P, Q, and K can be any integers (also perform multiplications for adjacent letters P, Q, K)
Y = 2PQK (Since either P or Q must be even, Y is always divisible by 4)
Z = (P2 + Q2)K (We won’t use this equation in the actual computer algorithm)
P, Q, and K can be any integers (also perform multiplications for adjacent letters P, Q, K)
For example, if we let P = 2, Q = 1, and K = 1, then we get X = 3, Y = 4, and Z = 5. This is the smallest possible integer right triangle.
We note that the “X” term above has three components: (P-Q), (P+Q), and K. If we are going to generate “odd” numbers for our trial bricks, then each of these components must be odd. For example, if we want to generate a trial brick where the odd side is equal to 85, then the 85 is separated into three components whose product equals 85. Here, the only two possibilities are 1 times 5 times 17 and 1 times 1 times 85. (These triplets can be in any order.) We will use these triplets to solve for “P”, “Q”, and “K”. In turn, we will use the results to generate the 85, 132, 720 example given earlier that “almost” solves the integer brick problem.
In the multiplication of 1 x 5 x 17 = 85, the 1, 5, and 17 factors can be in an order. However, the terms (P-Q)(P+Q)K require (P+Q) to be larger than (P-Q). Thus, for our multiplication, we only use permutations where the second term is larger than the first. We now have:
1 x 5 x 17 = 85
1 x 17 x 5 = 85
5 x 17 x 1 = 85
Each of these can be solved to get a “P”, “Q”, “K” triplet
If we let (P-Q) = 1 and (P+Q) = 5, then we get P = 3, Q = 2, and K = 17
Substituting these in Y = 2PQK yields Y = 204 (In practice, this result won’t be useful)
If we let (P-Q) = 1 and (P+Q) = 17, then we get P = 9, Q = 8, and K = 5
Substituting these in Y = 2PQK yields Y = 720 (One of the sides in our brick)
Finally, if we let (P-Q) = 5 and (P+Q) = 17, then we get P = 11 , Q = 6, and K = 1
Substituting these in Y = 2PQK yields Y = 132 (The other side that we used in the brick)
The only other valid multiplication is:
1 x 85 x 1 = 85
If we let (P-Q) = 1 and (P+Q) = 85, then we get P = 43, Q = 42, and K = 1
Substituting these in Y = 2PQK yields Y = 3612.
Thus we have found the four right triangles that can have one side equal to 85. The other side can equal 132, 204, 720, or 3612. (These are the only four. There are no others.)
These four results are then tried in various combinations for trial sides of the integer brick. You can reduce the trial combinations a great deal further by observing that if a solution exists, the “top-surface” diagonal would be one of the members of the above trial list.
In the above example, there are only 4 divisors of 85 (1, 5, 17, and 85). For other odd “X” sides, there may be many possible triplets. (e.g. If the odd number is a product of many small odd prime numbers.) Our more efficient algorithm thus becomes:
For “odd side” equals 3, 5, 7, etc.
Generate all possible triplets that can be multiplied to produce the odd number
For each valid permutation, solve for P, Q, K and the second side of a right triangle
Make a list of all of these trial “Side 2’s”
Search the list to see if any combination yields a solution
Repeat the above for the next odd number.
Finally, we have not mentioned an efficient way to find the “triplet” trial divisors. You could of course try dividing the “odd side” by 3, 5, 7, etc. up to Sqrt(odd number). This is not efficient.
A much faster way of finding trial divisors for the “triplets” can be found using a “sieve” algorithm. In the table below, note where the “1’s” show up.
Trial < - - - - Trial “Odd Numbers” - - - - >
Divs. 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 . . . 85 . . .
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
3 1 0 0 1 0 0 1 0 0 1 0 0 1 0 0 1 0 0
5 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 1
7 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0
9 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0
11 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0
13 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0
15 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0
17 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1
.
.
85 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
Etc.
The top row lists the trial odd numbers that will be used for the odd side of the brick. The left edge lists all odd numbers which potentially might be evenly divisible into the trial odd number.
All possible trial numbers are divisible by 1. We know that 3 can be divided by 3. Then we simply go three columns to the right of this number to find another trial odd number that is also divisible by 3. We can continue going right 3 columns at a time as far as needed.
A similar process works for Trial Divisor = 5. We just mark a “1” in every 5th column. The process can be extended for as many rows as needed. If you use this “sieve” method to find trial divisors, all you have to do is start a list for each column. Then process each row by adding a new divisor to the appropriate list each time a “1” would be encountered. (For computer science students, think “Link List”). Periodically, a large block of the table can be generated which will generate lists for large numbers of trial “Odd Numbers”.
In the program, a block for these divisor lists is 100,000 columns wide. (Trial “Odd Numbers” increase by 200,000 per block.) With Trial “Odd Numbers” in the 1.0E11 to 1.0E12 range, on average there are near to slightly over 6 divisors per column. Thus the program generates about (to a little over) 600,000 nodes in the divisor lists per block.
Exploring
the Great Unknown - The (Non) Results
The author wrote a computer program based on the algorithm outlined above. (Actually, a couple of different versions were used.) Initially, all odd numbers out to 21 billion were tried on a Pentium 4 computer. Subsequently, a Skulltrail computer was used to extend the search out to 3.0 trillion. (3.0E+12). All versions of the program were written in “C” and used the lcc-win32 C compiler system. (http://www.cs.virginia.edu/~lcc-win32/)
It should be noted that if the odd side of a right triangle is represented by the variable “X”, then the even side can be as large as (X2 -1)/2. Thus, if the odd side is 1.0E+12, the even side can be as large as 5.0E+23. This has more digits than the precision that exists on Intel processors. Then of course these numbers have to be squared for the X2 + Y2 calculations. Thus, the computer program has to keep track of the extra precision.
No solutions were found.
The best chance of finding a possible solution would appear to occur when the “odd side” of the brick is a product of many small factors. For example, at “odd side” = 9,704,539,845 (3x3x5x7x11x13x17x19x23x29) the program generated 16,402 right triangles that shared the same common odd edge. Even with this many candidates for the other dimensions of the brick, there were no combinations that produced a solution.
The possibility exists that the computer program is faulty, and a solution actually exists somewhere in the search range. Viewers are encouraged to launch their own search efforts in case a solution actually exists.
External
Solutions
An external solution consists of integer edges and integer external diagonals. One version of the program generated a disk file that contained all the external solutions with the 3 sides <= 1,000,000,000 with one side “odd”.
There were 4,631 of these which were subsequently read into a spreadsheet so that they could be “played with”. Click here if you would like to view/copy this list.
Various experiments were tried using Greatest Common Divisor, Mod 2 arithmetic, Mod 3 arithmetic, etc. (e.g. The product of the 3 dimensions is always divisible by 95,040.) No reliable pattern was recognized that would prevent a solution that would also include an integer internal diagonal.
The 7 external solutions with all 3 dimensions under 1,000 were given earlier. However, only 5 of these are primitive. (A primitive solution has no common divisor for the 3 edges.)
The following table shows the number of primitive external solutions where the 3 sides are no larger than the Dimension Limit.
Number of
Dimension Primitive
Limit Solutions
1,000 5
10,000 19
100,000 65
1,000,000 242
10,000,000 704
100,000,000 1,884
1,000,000,000 4,631
10,000,000,000 10,943
100,000,000,000 43,106
External solutions come in all shapes and sizes.
For example, there are long flat solutions:
X Y Z
74,745 23,085,952 186,227,160
Nearly cubical solutions:
X Y Z
110,562,771 108,192,528 109,141,700
Multiple solutions for a given height:
X Y Z
1,155 1,008 1,100
1,155 6,688 6,300
Source
Code
If anyone would like to view/use the “C” source code for the program, it is available here ( http://www.durangobill.com/IntBrickSourceCode.html ) It should compile “as is” using the lcc win32 “C” compiler. If you have any questions please feel free to ask. (My E-mail address is on my home page) If you publish any results that use the program (or derivatives thereof), I would appreciate an acknowledgement that I supplied the original code/algorithm.
If you compile and run the program, you will get a lot of output in the first few seconds. This will include a lot of status information. If you start the search at 0, this will also include external solutions with the odd side of the brick < 5000. However, things will quickly quiet down to just periodic status information after the first few seconds. (About as exciting as watching grass grow.)
If you find an error/bug in the program, please let me know so I can fix it and try again. (I’m pretty sure the program is OK, but there’s no 100% guarantee on these things.)
For additional information about the Euler Brick Problem please see:
Eric Weisstein’s "Perfect Cuboid" web page: http://mathworld.wolfram.com/PerfectCuboid.html
and
Fred Curtis’s "Primitive Euler Bricks" web page: http://f2.org/maths/peb.html
Return to Durango Bill's Home Page