Suppose that the dots/vertexes in the above diagram represent geographical locations that you wish to join in a fiber optic network. Fiber optic cable is expensive and therefore you would like to use the smallest possible total length. A further restriction is that junctions can only be made at the dot locations.

   Where should the fiber cable lines be installed to minimize the total cost? (For this problem, assume that distances/costs are on an X,Y coordinate system and cable lines can be installed as straight lines between the points.)

   This is a “Minimal Spanning Tree” problem. The answer is shown below.


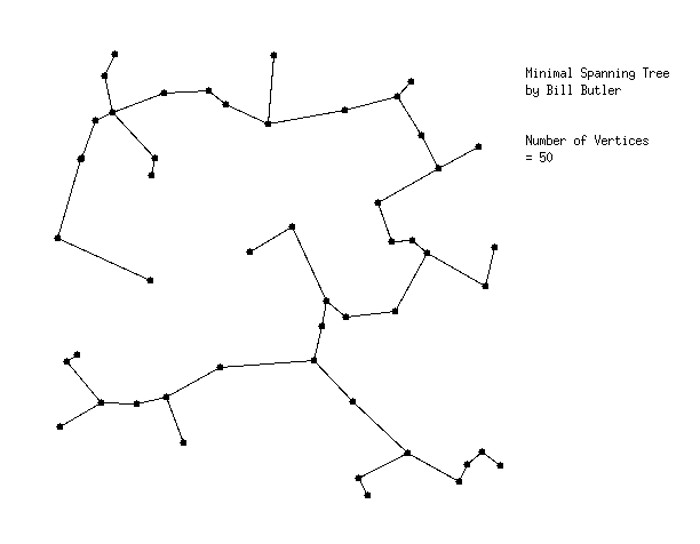
   The diagram above shows the minimal length pattern that should be used for the fiber optic cables.

   The general problem is called the “Minimal Spanning Tree” problem. A similar problem might be to connect various locations on an electronic circuit board.

   There are multiple computer algorithms that can be used to solve Minimal Spanning Tree problems. Sample computer code (in “C”) can be seen here.




   Minimal spanning tree computer programs can also be used to generate ordinary mazes.


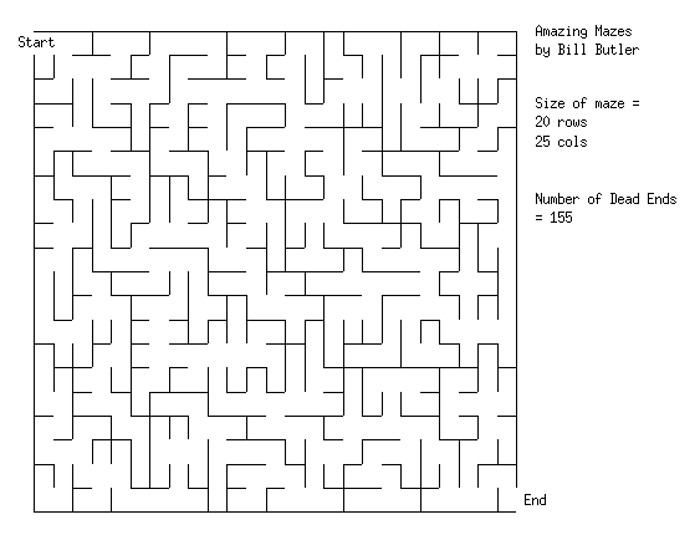
Click here to see a “somewhat more complex” maze.

Click here to see the solution to the “somewhat more complex” maze.

   It can be shown that the interior passageways in an ordinary maze are a spanning tree. You can start and end at any two random locations, and there is one and only one route that will connect the two locations.

An algorithm for creating a computer generated maze might be:

1) Start with a solid grid of lines. (For example, lines on  a piece of graph paper.)

2) Assign random weightings to all the minor interior edge lines in the grid.

3) Treat these weighted minor edges as the potential connections between the centers of the minor cells. (i. e. The center of each small cell in the grid is treated as if it were a vertex, and each weighted minor edge is a potential connection to an adjacent vertex/cell.)

4) Solve the minimal spanning tree problem.

5) Erase the minor edges in the grid that correspond to solution edges in the Minimal Spanning Tree problem.

6) Erase any 2 minor edges in the exterior lines of the grid. This creates “Start” and “End” positions.

7) You now have an ordinary maze.

Hint for programmers. In the maze version of the Minimal Spanning Tree problem, when a vertex/maze cell is added to the tree, there are a maximum of 3 potential edges to adjacent vertexes/cells. Try using a “heap” algorithm instead of the inner loop used in the code given in the earlier code link.



For another example of graphics programming, please see the author's web page at:
http://www.durangobill.com/TravelingSalesman/TravelingSalesman.html
The Traveling Salesman Problem





Web page generated via Sea Monkey's Composer HTML editor
within  a Linux Cinnamon Mint 18 operating system.
(Goodbye Microsoft)

Return to Durango Bill's home page