Game Rules: Pig (Pig-out) is a dice game for two or more players. (Some handheld computers include the game as a built-in feature.) There are two versions of the game. In one version, “pigs” and “pig-outs” occur when a player rolls the dice and gets at least one “1” on the dice. The other version is similar but uses “6’s” for the “Pigs” and “Pig-outs”.

Version 1 - “Pig” when a dice roll yields a single “1” and Pig-Out on double “1’s”

   A player rolls two dice, and if neither die shows a “1”, he uses the total to initialize his temporary score. At this point he has a choice of two actions. 1) He may add this temporary score to his previously recorded score and pass the dice to the next player (thereby ending his turn), or 2) roll the dice again.

   If he rolls again and still does not have a “1” on either die, the player adds the new dice total to his temporary score. The player may continue this process until he either voluntarily stops and records his score (adds his temporary score to his prior recorded score thereby producing a new, higher recorded score), or at some point in the sequence one of the dice rolls will show at least one “1”.

   If at any point in a player's turn, one of the dice shows a “1”, the entire temporary score is lost, and the dice are passed to the next player. However, the player still keeps his prior recorded score. Still worse, if double one’s (snake eyes) are rolled at any time, the player loses his entire score, his turn ends, and on his next turn he starts from zero (no recorded score).

The first player to reach 100 wins.

 
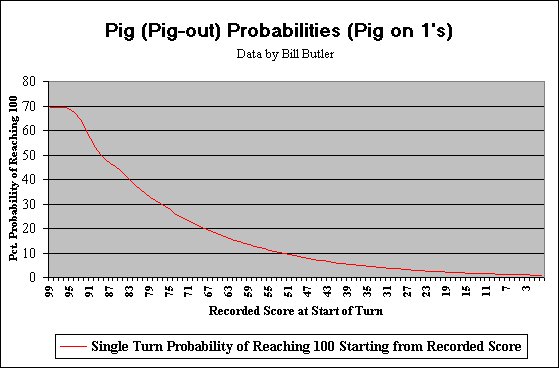
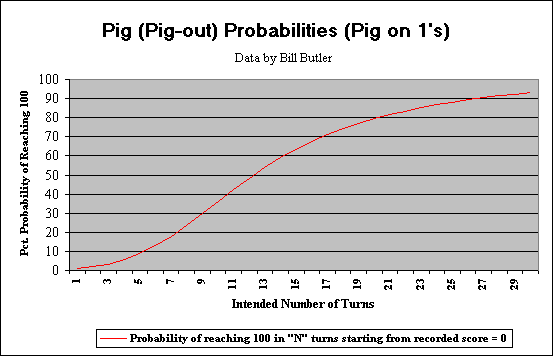
Pig1 Graphs: These two graphs display statistical probabilities. The first graph shows the probability of reaching 100 or better in a single turn given that you are starting from some given recorded score “R”. (Data is taken from the first column of the first table in the Pig 1 Statistics link.) For example: If you start your turn with a recorded score of 30, then there is a 3.6 percent probability you could roll the dice enough times to get to at least 100 before a “1” shows up on at least one of the dice.

   The second graph shows the probability of reaching 100 (or more) in “N” turns (using optimal strategy) if you start your turn with no recorded score (start of game status). Data for this graph is taken from the bottom row of the first table (uses both sections). For example: If you want to reach 100 in 10 (or less) turns and have no recorded score (start of game condition), then you have a 36.0 percent chance of success if you are using optimal strategy.


Pig1 Statistical Data and Optimal Strategy:  This link shows two tables - both of which are split into two parts due to their size. The first table shows the probability that you will reach 100 or better in “N” (or less) turns using optimal strategy given that you have some recorded score “R” at the start of a turn. The first part of this table displays data for 1 - 15 turns (column headers) while the second part shows results for 16 - 30 turns.

   The second table shows the optimal strategy, and again is split into two parts. If you want to reach 100 in “N” turns (column headers) and started your turn with the recorded score shown in the leftmost column, then you should continue to roll the dice until your temporary score (formed by summing the results of dice rolls on your current turn) reaches or exceeds the “Stop Number” shown in the table. (This assumes none of your dice rolls contains a “1”).

   For example: Lets assume you have a recorded score of 76 at the start of your turn and want to get to 100 (or more) in 3 (or less) turns. The optimal strategy is to roll the dice has long as your temporary sum is less than 15. If you achieve a temporary sum of 15 or higher, you should voluntarily stop, and add your temporary score to your previous recorded score. This will give you a new higher score that will be your starting point on your next turn.

   You should understand that the “optimal strategy” does not guarantee that you will successfully obtain your objective. What the “optimal strategy” does is give you the best chance of obtaining your objective. 
 
How to Calculate the Optimal Strategy:  This link outlines how to calculate the data in the Pig 1 tables. (How to calculate the Pig 6 statistics is not given but is very similar.) This involves some understanding of “Expected Values” and iterative algorithms used in designing a computer program that will execute some serious number crunching. It would be a suitable assignment for a college project (Junior or Senior level). If you are interested, just follow the link.
  
 

   The game rules are identical for this version of pig except the player loses his temporary turn score when one of the dice shows a “6”, and loses his entire score when double “6’s” (box cars) are rolled. However, in this version, it is more difficult to reach 100. Also, the optimal strategy changes.

 
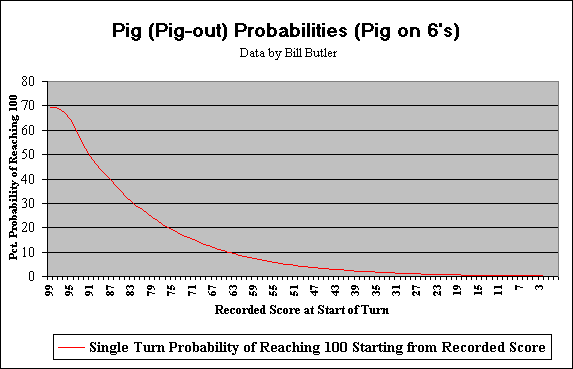
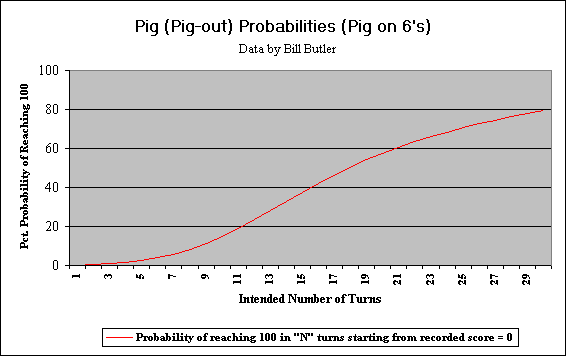
Pig6 Graphs: These two graphs display statistical probabilities. The first graph shows the probability of reaching 100 or better in a single turn given that you are starting from some given recorded score “R”. (Data is taken from the first column of the first table in the Pig 6 Statistics link.) For example: If you start your turn with a recorded score of 30, then there is a 1.3 percent probability you could roll the dice enough times to get to at least 100 before a “6” shows up on at least one of the dice.

   The second graph shows the probability of reaching 100 (or more) in “N” turns (using optimal strategy) if you start your turn with no recorded score (start of game status). Data for this graph is taken from the bottom row of the first table (uses both sections). For example: If you want to reach 100 in 10 (or less) turns and have no recorded score (start of game condition), then you have a 14.9 percent chance of success if you are using optimal strategy.

 
Pig6 Statistical Data and Optimal Strategy:  This link shows two tables - both of which are split into two parts due to their size. The first table shows the probability that you will reach 100 or better in “N” (or less) turns using optimal strategy given that you have some recorded score “R” at the start of a turn. The first part of this table displays data for 1 - 15 turns (column headers) while the second part shows results for 16 - 30 turns.

   The second table shows the optimal strategy, and again is split into two parts. If you want to reach 100 in “N” turns (column headers) and started your turn with the recorded score shown in the leftmost column, then you should continue to roll the dice until your temporary score (formed by summing the results of dice rolls on your current turn) reaches or exceeds the “Stop Number” shown in the table. (This assumes none of your dice rolls contains a “6”).

   For example: Lets assume you have a recorded score of 76 at the start of your turn and want to get to 100 (or more) in 3 (or less) turns. The optimal strategy is to roll the dice has long as your temporary sum is less than 15. If you achieve a temporary sum of 15 or higher, you should voluntarily stop, and add your temporary score to your previous recorded score. This will give you a new higher score that will be your starting point on your next turn.

   You should understand that the “optimal strategy” does not guarantee that you will successfully obtain your objective. What the “optimal strategy” does is give you the best chance of obtaining your objective.
 
 

   In the above paragraphs, we have referred to using “N” turns to reach 100 or better. In practice (in a game) you as a player have to determine how many turns you should use to try to get to 100. If you have a score of 20 and an opponent has 80, it is fairly obvious that you should follow an aggressive strategy that has the best chance of getting to 100 in “just a few” turns. Alternately, if YOU have the 80 and your opponent has 20, you can allow more leeway and take “a few more turns”. The first statistical table will give some guidance as to how long it will take your opponent to get to 100, but most of the time you must make “an intelligent guess” based on experience, the other player's strategy, etc.

   Many games fall into the “I win - you lose” or “I lose - you win” category. These games are referred to as “Two person - zero sum” games. What one side wins, the other side loses. Games of this type can usually be analyzed by “Minimax” theory. Your objective is to minimize your opponent’s chance of winning (thereby maximizing your chances) while your opponent is trying to maximize his chance of winning and minimize yours. We will examine this concept for 1 round of chess and touch on how it could be applied to Pig.

   Let's assume you are playing chess and have 3 possible moves. For each of your 3 possible moves (Let’s call them A, B, and C), your opponent has 3 possible answering moves (Let’s call your opponents possible moves 1, 2, and 3). It is your turn to play, and you wish to make the best move.

   First, we generate all 9 possible sequences and evaluate the board position for each. We will award a numerical score for each of these positions where increasing positive values indicate a favorable position for you while negative values favor your opponent.

     Move       Board
   Sequence     Score
   ------------------
      A1          0
      A2         -1
      A3          6
      B1         -2
      B2         -3
      B3         -4
      C1          1
      C2          2
      C3          3

  If you make move “A”, your opponent will make the move that will minimize your score thus maximizing his score. Hence your opponent will make move “2” which will leave you with a losing “-1” position.

   If you make move “B”, your opponent will again make the move that maximizes his position thereby minimizing the value of your position. Thus, if you make move “B” your opponent will make move “3” leaving you with a “-4”.

   Finally, if you make move “C”, the best your opponent can do is respond with a “1”. This will leave you with a “1”. Thus, the choices (A, B, C) for you will generate a “ -1”, “ -4”, or “ +1”. You want to find the best combination (maximize from among these choices). Your best move is thus “C”.


   If we apply this principle to “Pig” the discrete moves of chess are replaced by the optimal strategies that would have to be computed for each of the possible “luck” combinations of the dice rolls (and their associated probabilities). This might be of mathematical interest, but the “luck” factor severely complicates the combinatorics to the point where the only possible game would be computer vs. computer.



Return to Durango Bill's Home Page
 

Web page generated via Sea Monkey's Composer HTML editor
within  a Linux Cinnamon Mint 18 operating system.
(Goodbye Microsoft)