
Durango Bill's
"Shut The Box" Analysis
Mathematical Analysis and Optimal Strategy for Several
Variations of the Dice Game "Shut The Box" - including casino/high stakes possibilities
Game
Rules: The game consists of a pair of dice and
markers (boxes) for the digits 1 to 9. A player rolls the dice
and uses the total in any way that he sees fit to "shut" or
otherwise mark one or more of the digits (boxes) as used. For
example, if the dice total is 9, any of the following
combinations may be used: 9, 1&8, 2&7, 3&6,
4&5, 1&2&6, 1&3&5, 2&3&4.
Then the dice are rolled again and the new total is used to mark additional digits as used. However, each digit may be used only once with the result the choices become increasingly constricted as the game progresses. If a player has remaining digits totaling 6 or less (sum of the flipped digits >= 39), then only one die is used. The game ends when the current dice (die) total has no remaining combinations that can be used. A perfect game occurs if all nine digits (sum = 45) are flipped.
There are many versions of the game including the name. These other names include Canoga, Klackers, Batten down the Hatches, High Rollers), etc. Please see http://en.wikipedia.org/wiki/Shut_the_Box for more information.
Scoring: Scoring for the game consists of adding together all the flipped (used) digits. If all nine digits are used, then their sum is 45, which represents the best possible score. An alternate method of scoring adds up the total for all the boxes that haven’t been flipped. If you use this method of scoring, then a perfect game has a score of zero. (Nothing left to be flipped.)
Casino style payouts can be used with a default payout of 100 awarded for a perfect score of 45. All other scores are awarded zero. This payout schedule optimizes the game for an "all or nothing win", and the calculated "Expected Value" for any mid-game position becomes the probability (in percent) that the game will be won given the current status of the flipped digits. Alternately, smaller payouts could be awarded for "close but not quite". (Changing the payout table also changes the optimal strategy).
Game Variations: In addition to the standard game described above, there are several variations of "Shut the Box". In one variation, the player always uses two dice. Another variation uses one die if the sum of the flipped digits is >= 39, but the number of digits that can be flipped on any dice roll is limited to two. Thus, if the player rolls a "9" the combinations 1&2&6, 1&3&5, 2&3&4 can not be used.
Finally, it is possible to design a high-jackpot casino style game (use real money).
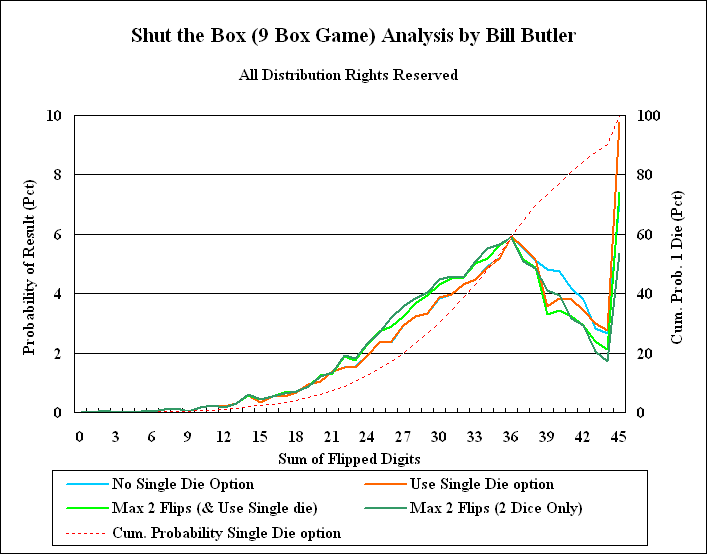
Statistics Data and Graph: The Statistical Data link displays a table showing the probability of any given final (end of game) score assuming the player is using optimal strategy to maximize the winning probability. The above graph summarizes the probabilities for all four different game variations.
If you are using the “use 1 die at 39 or higher game option”, the red line shows the probabilities for ending at any given score assuming that you are using optimal strategy to play for a win. Using optimal strategy there is a 9.7614% chance that you will win. If you always use two dice (blue line), there is only a 7.1432% chance that you will win. Note that without the “1 die” option, there are higher probabilities of getting stuck just short of winning. The light green line shows the probabilities if you can never flip more than two boxes at a time, but are allowed to shift to 1 die if your score is 39 or higher. Here, there is a 7.4194% chance of winning. Finally, the dark green line shows the probabilities if you always have to use two dice and can not shut more than 2 boxes at a time. This final version has only a 5.3488% chance of winning.
Several casinos/online betting houses let you play Shut the Box for real money. The table below shows the statistics (using optimal strategy) for a sample game that always uses 2 dice, limits box closings to a maximum of 2 per dice toss, and pays double if you win with a dice toss of doubles. The Payout Amounts per $1.00 bet are based on Ladbrokes’ online Shut the Box game. (Payout amounts as of Aug. 17, 2010) Optimal strategy for this game can be seen here: http://www.durangobill.com/ShutTheBoxExtra/STB_Ladbrokes_Strategy.html
Payout
Not Amount Final Cumulative Cumulative
Flipped Flipped per $1 Score Score Value Value
Total Total Bet Probability Probability Contribution Contribution
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
2 43 0.00 0.0008 0.0008 0.0000 0.0000
3 42 0.00 0.0000 0.0008 0.0000 0.0000
4 41 0.00 0.0000 0.0008 0.0000 0.0000
5 40 0.00 0.0003 0.0010 0.0000 0.0000
6 39 0.00 0.0004 0.0014 0.0000 0.0000
7 38 0.00 0.0009 0.0024 0.0000 0.0000
8 37 0.00 0.0012 0.0035 0.0000 0.0000
9 36 0.00 0.0004 0.0039 0.0000 0.0000
10 35 0.00 0.0017 0.0056 0.0000 0.0000
11 34 0.00 0.0022 0.0078 0.0000 0.0000
12 33 0.00 0.0015 0.0094 0.0000 0.0000
13 32 0.00 0.0030 0.0123 0.0000 0.0000
14 31 0.00 0.0061 0.0184 0.0000 0.0000
15 30 0.00 0.0044 0.0229 0.0000 0.0000
16 29 0.00 0.0053 0.0282 0.0000 0.0000
17 28 0.00 0.0061 0.0343 0.0000 0.0000
18 27 0.00 0.0072 0.0415 0.0000 0.0000
19 26 0.00 0.0087 0.0501 0.0000 0.0000
20 25 0.10 0.0123 0.0625 0.0012 0.0012
21 24 0.10 0.0133 0.0758 0.0013 0.0026
22 23 0.10 0.0187 0.0945 0.0019 0.0044
23 22 0.10 0.0182 0.1127 0.0018 0.0063
24 21 0.10 0.0228 0.1355 0.0023 0.0085
25 20 0.10 0.0269 0.1625 0.0027 0.0112
26 19 0.10 0.0289 0.1914 0.0029 0.0141
27 18 0.30 0.0327 0.2241 0.0098 0.0239
28 17 0.30 0.0365 0.2605 0.0109 0.0349
29 16 0.30 0.0386 0.2991 0.0116 0.0464
30 15 0.30 0.0428 0.3419 0.0128 0.0593
31 14 0.30 0.0451 0.3871 0.0135 0.0728
32 13 0.30 0.0457 0.4328 0.0137 0.0865
33 12 0.50 0.0514 0.4841 0.0257 0.1122
34 11 0.50 0.0517 0.5358 0.0258 0.1381
35 10 0.50 0.0553 0.5912 0.0277 0.1657
36 9 0.50 0.0558 0.6470 0.0279 0.1937
37 8 1.00 0.0520 0.6990 0.0520 0.2457
38 7 1.00 0.0485 0.7475 0.0485 0.2942
39 6 1.00 0.0438 0.7913 0.0438 0.3380
40 5 1.00 0.0396 0.8310 0.0396 0.3776
41 4 2.50 0.0377 0.8687 0.0943 0.4720
42 3 2.50 0.0350 0.9037 0.0874 0.5594
43 2 2.50 0.0232 0.9268 0.0579 0.6173
44 1 2.50 0.0226 0.9495 0.0566 0.6739
45 0 5.00 0.0434 0.9929 0.2171 0.8909
45 Dbls 0 10.00 0.0071 1.0000 0.0711 0.9620
This sample casino game will return about $0.9620 for every dollar that you bet. Note: The above long term payout rate has been confirmed via billions of computer generated games.
Optimal Strategies: The optimal strategy pages for the Standard Game, Always use two dice, Max 2 flips, and 12-box (always use 2 dice) variations show the best flip strategy given any interim status of flipped digits and the current dice roll. The "Expected Value" for each position shows the probability of winning (expressed as a percent) given the current combination of flipped digits. (Allow a minute to download the table.)
Casino Style "Shut the Box": This link describes a possible variation of the game that could be played using real money in a high-jackpot casino game (or possibly a web based equivalent). (Any manufacturer or web developer interested?)
Another variation of Shut the Box uses 12 boxes instead of 9. There are no standard rules for the 12 box version, but the analysis given here assumes that you always use 2 dice. As shown below, it is much more difficult to shut all 12 boxes. The probability of winning is only 0.3622 percent. (One chance in 276.) A possible variation of the game might instead use 3 dice until a score of 50 is reached, then use 2 dice up through a score of 71, and then use 1 die if your score is 72 or higher.
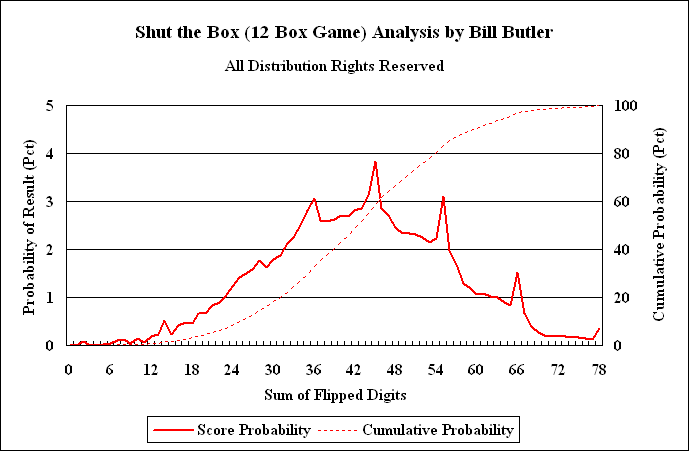
The graph above shows the probability of various outcomes for the 12-box game. (Assumes that you are using optimal strategy to maximize your chance of winning the game.) The dashed line shows the probability that your game will end by the time you get to the indicated score. For example, there is about an 83.355 percent chance that your game will end on or before the total of your flipped boxes reaches the spike at 55.
The solid line shows the probability that your game will end at a specific score. (The score is the sum of the flipped boxes.) For example, if you are using optimal strategy to try to win the game, there is a 3.83 percent probability that your game will end when the sum of your flipped boxes is exactly 45.
The spikes in the probabilities for scores of 36, 45, 55, and 66 are of interest. First of all, the spikes are real and not computational or plotting errors. The theoretical probabilities (plotted above) were tested by running tens of millions of random games using different random dice sequences. The random tests produced similar spikes. (At 10,000,000 games the standard statistical test of +/- 2 standard deviations has a magnitude of about 0.01 on the left graph axis.) The probability spikes also show up at the same locations when the dice are weighted and the “Payoff Table” is set for the previously mentioned “Casino Style Shut the Box” game.
We note that 36 is the sum of the digits from 1 through 8, 45 is sum of the digits from 1 through 9, etc. If you toss a pair of dice, two out of three times you will get a 5, 6, 7, 8, or 9. It is easy to use these results to flip boxes with mid-sized or low numbers. It is significantly more difficult to flip higher numbered boxes. Thus the game tends to end after you have flipped all the low to mid sized numbers, and never have a chance to flip the higher numbers.
Still another variation of Shut the Box uses a single 12-sided die (a dodecahedron) for the 12 box game. If you use only one of these dice instead of 2, it increases the probability that the game will end with you having a very low or very high score, and decreases the probability that you will have a middle sized score. The probability of winning increases from 0.3622 percent for the 2-dice version to 0.6659 percent for this one 12-sided die version. (One chance in 150)
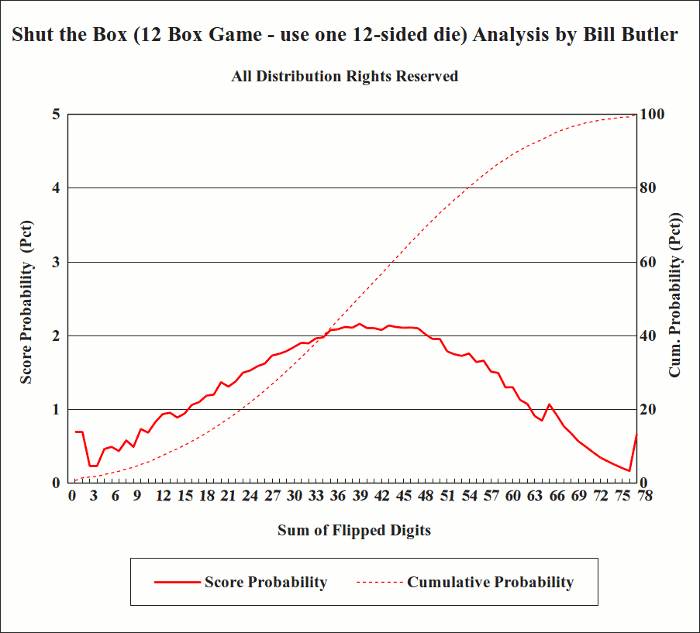
The graph above shows the probability of various outcomes for the one 12-sided die, 12-box game. (Assumes that you are using optimal strategy to maximize your chance of winning the game.) The dashed line shows the probability that your game will end by the time you get to the indicated score.
The solid line shows the probability that your game will end at a specific score. (The score is the sum of the flipped boxes.) For example, if you are using optimal strategy to try to win the game, there is a 2.16 % chance that the game will end when the sum of your flipped boxes is 40. While this is the most likely final score, there is a broad range of likely other final scores that run from the 20s to the 50s.
The optimal strategy table for the 12-sided game can been seen here. Given the boxes that have been flipped (leftmost column) and the outcome of the current roll of the 12-sided die (top row), the digits in the table show what strategy to use.
For example:
Assume that you rolled an "8" on the first die roll and flipped the "8" box. Then assume that you rolled another "8" on your 2nd roll. Since the "8" is no longer usable, you have four choices.
1) Flip 1 & 7
2) Flip 2 & 6
3) Flip 3 & 5
4) Flip 1 & 2 & 5
5) Flip 1 & 3 & 4
If you go down the left column until you see a single "8" (This is what has already been flipped) and then to the right until you are under your current die roll of "8", you will see "35". This means the optimal choice for using your current roll of "8" is to flip boxes 3 and 5.
If you use the "Expected Value" column, you can see why "3 & 5" is the optimal choice. The list below shows the 5 possible outcomes that might result from the above choices. (Expected Value shows the percent chance of winning)
Boxes Expected
Flipped Value
178 0.30
268 0.31
358 0.34
1258 0.07
1348 0.10
From the 5 possible choices, your best chance of winning is to complete your turn with boxes 3, 5, & 8 flipped. (It took a computer program using "Dynamic Programming" to calculate those Expected Value numbers.)
There is still another variation of Shut the Box that uses 10 boxes. As with the 12-box version, there are no standard rules for the 10 box version. Again, the analysis given here assumes that you always use 2 dice. It is more difficult to win the 10 box game than the 9-box game, but it is no where near as difficult as the 12 box game. If you use optimal strategy, the probability of winning is 4.0361 percent. (About one chance in 25.)
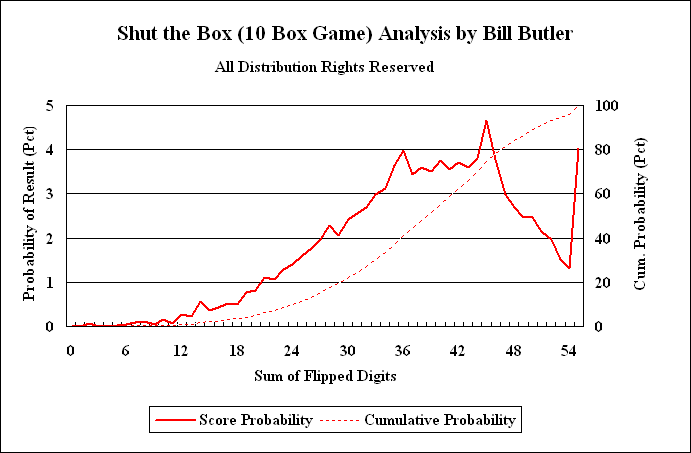
The graph above shows the probability of various outcomes for the 10-box game. (Assumes that you are using optimal strategy to maximize your chance of winning the game.) The dashed line shows the probability that your game will end by the time you get to the indicated score. For example, there is about a 74.621 percent chance that your game will end on or before the total of your flipped boxes reaches 45.
The solid line shows the probability that your game will end at a specific score. (The score is the sum of the flipped boxes.) For example, if you are using optimal strategy to try to win the game, there is a 4.665 percent probability that your game will end when the sum of your flipped boxes is exactly 45.
As we observed in the 12-box game, spikes in the probable results show up at 36 and 45. The spike at 36 indicates that you may have flipped all the boxes from 1 to 8, but you probably were not able to flip boxes 9 or 10. The spike at 45 is similar, but it is the sum of flipping boxes 1 to 9.
Return to Durango Bill's Home Page
Web page generated via Sea Monkey's Composer HTML editor
within a Linux Cinnamon Mint 18 operating system.
(Goodbye Microsoft)
Then the dice are rolled again and the new total is used to mark additional digits as used. However, each digit may be used only once with the result the choices become increasingly constricted as the game progresses. If a player has remaining digits totaling 6 or less (sum of the flipped digits >= 39), then only one die is used. The game ends when the current dice (die) total has no remaining combinations that can be used. A perfect game occurs if all nine digits (sum = 45) are flipped.
There are many versions of the game including the name. These other names include Canoga, Klackers, Batten down the Hatches, High Rollers), etc. Please see http://en.wikipedia.org/wiki/Shut_the_Box for more information.
Scoring: Scoring for the game consists of adding together all the flipped (used) digits. If all nine digits are used, then their sum is 45, which represents the best possible score. An alternate method of scoring adds up the total for all the boxes that haven’t been flipped. If you use this method of scoring, then a perfect game has a score of zero. (Nothing left to be flipped.)
Casino style payouts can be used with a default payout of 100 awarded for a perfect score of 45. All other scores are awarded zero. This payout schedule optimizes the game for an "all or nothing win", and the calculated "Expected Value" for any mid-game position becomes the probability (in percent) that the game will be won given the current status of the flipped digits. Alternately, smaller payouts could be awarded for "close but not quite". (Changing the payout table also changes the optimal strategy).
Game Variations: In addition to the standard game described above, there are several variations of "Shut the Box". In one variation, the player always uses two dice. Another variation uses one die if the sum of the flipped digits is >= 39, but the number of digits that can be flipped on any dice roll is limited to two. Thus, if the player rolls a "9" the combinations 1&2&6, 1&3&5, 2&3&4 can not be used.
Finally, it is possible to design a high-jackpot casino style game (use real money).

Statistics Data and Graph: The Statistical Data link displays a table showing the probability of any given final (end of game) score assuming the player is using optimal strategy to maximize the winning probability. The above graph summarizes the probabilities for all four different game variations.
If you are using the “use 1 die at 39 or higher game option”, the red line shows the probabilities for ending at any given score assuming that you are using optimal strategy to play for a win. Using optimal strategy there is a 9.7614% chance that you will win. If you always use two dice (blue line), there is only a 7.1432% chance that you will win. Note that without the “1 die” option, there are higher probabilities of getting stuck just short of winning. The light green line shows the probabilities if you can never flip more than two boxes at a time, but are allowed to shift to 1 die if your score is 39 or higher. Here, there is a 7.4194% chance of winning. Finally, the dark green line shows the probabilities if you always have to use two dice and can not shut more than 2 boxes at a time. This final version has only a 5.3488% chance of winning.
Online/Casino
(real money) analysis
Several casinos/online betting houses let you play Shut the Box for real money. The table below shows the statistics (using optimal strategy) for a sample game that always uses 2 dice, limits box closings to a maximum of 2 per dice toss, and pays double if you win with a dice toss of doubles. The Payout Amounts per $1.00 bet are based on Ladbrokes’ online Shut the Box game. (Payout amounts as of Aug. 17, 2010) Optimal strategy for this game can be seen here: http://www.durangobill.com/ShutTheBoxExtra/STB_Ladbrokes_Strategy.html
Payout
Not Amount Final Cumulative Cumulative
Flipped Flipped per $1 Score Score Value Value
Total Total Bet Probability Probability Contribution Contribution
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
2 43 0.00 0.0008 0.0008 0.0000 0.0000
3 42 0.00 0.0000 0.0008 0.0000 0.0000
4 41 0.00 0.0000 0.0008 0.0000 0.0000
5 40 0.00 0.0003 0.0010 0.0000 0.0000
6 39 0.00 0.0004 0.0014 0.0000 0.0000
7 38 0.00 0.0009 0.0024 0.0000 0.0000
8 37 0.00 0.0012 0.0035 0.0000 0.0000
9 36 0.00 0.0004 0.0039 0.0000 0.0000
10 35 0.00 0.0017 0.0056 0.0000 0.0000
11 34 0.00 0.0022 0.0078 0.0000 0.0000
12 33 0.00 0.0015 0.0094 0.0000 0.0000
13 32 0.00 0.0030 0.0123 0.0000 0.0000
14 31 0.00 0.0061 0.0184 0.0000 0.0000
15 30 0.00 0.0044 0.0229 0.0000 0.0000
16 29 0.00 0.0053 0.0282 0.0000 0.0000
17 28 0.00 0.0061 0.0343 0.0000 0.0000
18 27 0.00 0.0072 0.0415 0.0000 0.0000
19 26 0.00 0.0087 0.0501 0.0000 0.0000
20 25 0.10 0.0123 0.0625 0.0012 0.0012
21 24 0.10 0.0133 0.0758 0.0013 0.0026
22 23 0.10 0.0187 0.0945 0.0019 0.0044
23 22 0.10 0.0182 0.1127 0.0018 0.0063
24 21 0.10 0.0228 0.1355 0.0023 0.0085
25 20 0.10 0.0269 0.1625 0.0027 0.0112
26 19 0.10 0.0289 0.1914 0.0029 0.0141
27 18 0.30 0.0327 0.2241 0.0098 0.0239
28 17 0.30 0.0365 0.2605 0.0109 0.0349
29 16 0.30 0.0386 0.2991 0.0116 0.0464
30 15 0.30 0.0428 0.3419 0.0128 0.0593
31 14 0.30 0.0451 0.3871 0.0135 0.0728
32 13 0.30 0.0457 0.4328 0.0137 0.0865
33 12 0.50 0.0514 0.4841 0.0257 0.1122
34 11 0.50 0.0517 0.5358 0.0258 0.1381
35 10 0.50 0.0553 0.5912 0.0277 0.1657
36 9 0.50 0.0558 0.6470 0.0279 0.1937
37 8 1.00 0.0520 0.6990 0.0520 0.2457
38 7 1.00 0.0485 0.7475 0.0485 0.2942
39 6 1.00 0.0438 0.7913 0.0438 0.3380
40 5 1.00 0.0396 0.8310 0.0396 0.3776
41 4 2.50 0.0377 0.8687 0.0943 0.4720
42 3 2.50 0.0350 0.9037 0.0874 0.5594
43 2 2.50 0.0232 0.9268 0.0579 0.6173
44 1 2.50 0.0226 0.9495 0.0566 0.6739
45 0 5.00 0.0434 0.9929 0.2171 0.8909
45 Dbls 0 10.00 0.0071 1.0000 0.0711 0.9620
This sample casino game will return about $0.9620 for every dollar that you bet. Note: The above long term payout rate has been confirmed via billions of computer generated games.
Optimal Strategies: The optimal strategy pages for the Standard Game, Always use two dice, Max 2 flips, and 12-box (always use 2 dice) variations show the best flip strategy given any interim status of flipped digits and the current dice roll. The "Expected Value" for each position shows the probability of winning (expressed as a percent) given the current combination of flipped digits. (Allow a minute to download the table.)
Casino Style "Shut the Box": This link describes a possible variation of the game that could be played using real money in a high-jackpot casino game (or possibly a web based equivalent). (Any manufacturer or web developer interested?)
12-Box Shut
the Box
Another variation of Shut the Box uses 12 boxes instead of 9. There are no standard rules for the 12 box version, but the analysis given here assumes that you always use 2 dice. As shown below, it is much more difficult to shut all 12 boxes. The probability of winning is only 0.3622 percent. (One chance in 276.) A possible variation of the game might instead use 3 dice until a score of 50 is reached, then use 2 dice up through a score of 71, and then use 1 die if your score is 72 or higher.

The graph above shows the probability of various outcomes for the 12-box game. (Assumes that you are using optimal strategy to maximize your chance of winning the game.) The dashed line shows the probability that your game will end by the time you get to the indicated score. For example, there is about an 83.355 percent chance that your game will end on or before the total of your flipped boxes reaches the spike at 55.
The solid line shows the probability that your game will end at a specific score. (The score is the sum of the flipped boxes.) For example, if you are using optimal strategy to try to win the game, there is a 3.83 percent probability that your game will end when the sum of your flipped boxes is exactly 45.
The spikes in the probabilities for scores of 36, 45, 55, and 66 are of interest. First of all, the spikes are real and not computational or plotting errors. The theoretical probabilities (plotted above) were tested by running tens of millions of random games using different random dice sequences. The random tests produced similar spikes. (At 10,000,000 games the standard statistical test of +/- 2 standard deviations has a magnitude of about 0.01 on the left graph axis.) The probability spikes also show up at the same locations when the dice are weighted and the “Payoff Table” is set for the previously mentioned “Casino Style Shut the Box” game.
We note that 36 is the sum of the digits from 1 through 8, 45 is sum of the digits from 1 through 9, etc. If you toss a pair of dice, two out of three times you will get a 5, 6, 7, 8, or 9. It is easy to use these results to flip boxes with mid-sized or low numbers. It is significantly more difficult to flip higher numbered boxes. Thus the game tends to end after you have flipped all the low to mid sized numbers, and never have a chance to flip the higher numbers.
12-Box (Using
one 12-sided die) Shut the Box
Still another variation of Shut the Box uses a single 12-sided die (a dodecahedron) for the 12 box game. If you use only one of these dice instead of 2, it increases the probability that the game will end with you having a very low or very high score, and decreases the probability that you will have a middle sized score. The probability of winning increases from 0.3622 percent for the 2-dice version to 0.6659 percent for this one 12-sided die version. (One chance in 150)

The graph above shows the probability of various outcomes for the one 12-sided die, 12-box game. (Assumes that you are using optimal strategy to maximize your chance of winning the game.) The dashed line shows the probability that your game will end by the time you get to the indicated score.
The solid line shows the probability that your game will end at a specific score. (The score is the sum of the flipped boxes.) For example, if you are using optimal strategy to try to win the game, there is a 2.16 % chance that the game will end when the sum of your flipped boxes is 40. While this is the most likely final score, there is a broad range of likely other final scores that run from the 20s to the 50s.
The optimal strategy table for the 12-sided game can been seen here. Given the boxes that have been flipped (leftmost column) and the outcome of the current roll of the 12-sided die (top row), the digits in the table show what strategy to use.
For example:
Assume that you rolled an "8" on the first die roll and flipped the "8" box. Then assume that you rolled another "8" on your 2nd roll. Since the "8" is no longer usable, you have four choices.
1) Flip 1 & 7
2) Flip 2 & 6
3) Flip 3 & 5
4) Flip 1 & 2 & 5
5) Flip 1 & 3 & 4
If you go down the left column until you see a single "8" (This is what has already been flipped) and then to the right until you are under your current die roll of "8", you will see "35". This means the optimal choice for using your current roll of "8" is to flip boxes 3 and 5.
If you use the "Expected Value" column, you can see why "3 & 5" is the optimal choice. The list below shows the 5 possible outcomes that might result from the above choices. (Expected Value shows the percent chance of winning)
Boxes Expected
Flipped Value
178 0.30
268 0.31
358 0.34
1258 0.07
1348 0.10
From the 5 possible choices, your best chance of winning is to complete your turn with boxes 3, 5, & 8 flipped. (It took a computer program using "Dynamic Programming" to calculate those Expected Value numbers.)
10-Box Shut
the Box
There is still another variation of Shut the Box that uses 10 boxes. As with the 12-box version, there are no standard rules for the 10 box version. Again, the analysis given here assumes that you always use 2 dice. It is more difficult to win the 10 box game than the 9-box game, but it is no where near as difficult as the 12 box game. If you use optimal strategy, the probability of winning is 4.0361 percent. (About one chance in 25.)

The graph above shows the probability of various outcomes for the 10-box game. (Assumes that you are using optimal strategy to maximize your chance of winning the game.) The dashed line shows the probability that your game will end by the time you get to the indicated score. For example, there is about a 74.621 percent chance that your game will end on or before the total of your flipped boxes reaches 45.
The solid line shows the probability that your game will end at a specific score. (The score is the sum of the flipped boxes.) For example, if you are using optimal strategy to try to win the game, there is a 4.665 percent probability that your game will end when the sum of your flipped boxes is exactly 45.
As we observed in the 12-box game, spikes in the probable results show up at 36 and 45. The spike at 36 indicates that you may have flipped all the boxes from 1 to 8, but you probably were not able to flip boxes 9 or 10. The spike at 45 is similar, but it is the sum of flipping boxes 1 to 9.
Return to Durango Bill's Home Page
Web page generated via Sea Monkey's Composer HTML editor
within a Linux Cinnamon Mint 18 operating system.
(Goodbye Microsoft)