
Durango Bill's
Enumeration of Trees
Enumeration of Structurally Different Rooted (oriented) Trees
Enumeration of Structurally Different Non-rooted (free) Trees
A tree is a graph
connecting "N" vertices with "N-1" edges such that there is
one and only one route between any two given vertices.
In a rooted tree, travel along any of the edges is directed toward the "root". The root is customarily the top vertex in the tree. A family tree is an example of a rooted tree where a single individual in the present generation has a branching tree of ancestors (root will be at the bottom). Alternately, a family tree may show the many descendants that started from a single ancestor (or marriage).
A non-rooted tree has a free form where no vertex has priority. A non-rooted tree can be twisted, deformed, contorted, etc. into many shapes without altering its structure.
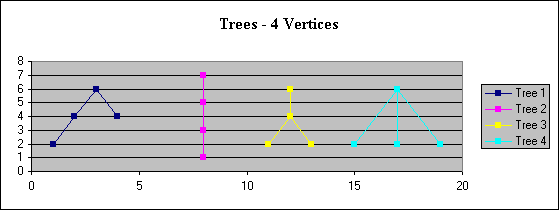
The chart above shows the 4 structurally different rooted trees (root is at the top) that can be constructed with 4 vertices. If we consider them as non-rooted trees, then there are only two different structures. Trees 1 and 2 have the same basic structure if there is no root. Similarly, trees 3 and 4 have the same non-rooted structure.
In a rooted tree, travel along any of the edges is directed toward the "root". The root is customarily the top vertex in the tree. A family tree is an example of a rooted tree where a single individual in the present generation has a branching tree of ancestors (root will be at the bottom). Alternately, a family tree may show the many descendants that started from a single ancestor (or marriage).
A non-rooted tree has a free form where no vertex has priority. A non-rooted tree can be twisted, deformed, contorted, etc. into many shapes without altering its structure.
The chart above shows the 4 structurally different rooted trees (root is at the top) that can be constructed with 4 vertices. If we consider them as non-rooted trees, then there are only two different structures. Trees 1 and 2 have the same basic structure if there is no root. Similarly, trees 3 and 4 have the same non-rooted structure.
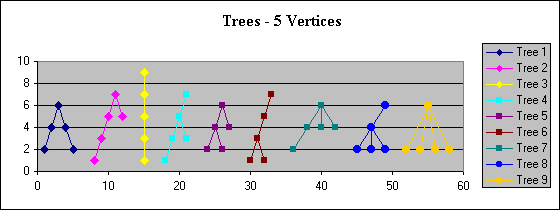
The chart above
shows the 9 structurally different rooted trees that are
possible if we use 5 vertices. If we use them as "free"
non-rooted trees, then there are only 3 structurally different
patterns. Trees 1, 2, and 3 are structurally the same if there
isn't a root. Similarly, trees 4, 5, 6, and 7 are all
variations of the same structure if there isn't a root.
Finally trees 8 and 9 have the same non-rooted structure.
An interesting question arises. If you have any "N" number of vertices connected by "N-1" edges, how many structurally different trees are there of each type? We will present the results followed by a source that viewers can check if they want to know how to calculate the results.
Number of structurally different, rooted and non-rooted trees
Computer Program by Bill Butler
Number of Number of Number of
Vertices Rooted Trees Non-rooted trees
-----------------------------------------------------------------
1 1 1
2 1 1
3 2 1
4 4 2
5 9 3
6 20 6
7 48 11
8 115 23
9 286 47
10 719 106
11 1,842 235
12 4,766 551
13 12,486 1,301
14 32,973 3,159
15 87,811 7,741
16 235,381 19,320
17 634,847 48,629
18 1,721,159 123,867
19 4,688,676 317,955
20 12,826,228 823,065
21 35,221,832 2,144,505
22 97,055,181 5,623,756
23 268,282,855 14,828,074
24 743,724,984 39,299,897
25 2,067,174,645 104,636,890
26 5,759,636,510 279,793,450
27 16,083,734,329 751,065,460
28 45,007,066,269 2,023,443,032
29 126,186,554,308 5,469,566,585
30 354,426,847,597 14,830,871,802
31 997,171,512,998 40,330,829,030
32 2,809,934,352,700 109,972,410,221
33 7,929,819,784,355 300,628,862,480
34 22,409,533,673,568 823,779,631,721
35 63,411,730,258,053 2,262,366,343,746
36 179,655,930,440,464 6,226,306,037,178
37 509,588,049,810,620 17,169,677,490,714
38 1,447,023,384,581,029 47,436,313,524,262
39 4,113,254,119,923,150 131,290,543,779,126
40 11,703,780,079,612,453 363,990,257,783,343
41 33,333,125,878,283,632 1,010,748,076,717,151
42 95,020,085,893,954,917 2,810,986,483,493,475
43 271,097,737,169,671,824 7,828,986,221,515,605
44 774,088,023,431,472,074 21,835,027,912,963,086
45 2,212,039,245,722,726,118 60,978,390,985,918,906
46 6,325,843,306,177,425,928 170,508,699,155,987,862
47 1.8103E+19 477,355,090,753,926,459
48 5.1842E+19 1,337,946,100,045,842,280
49 1.4856E+20 3,754,194,185,716,399,992
50 4.2598E+20 1.0545E+19
100 5.1384E+43 6.3013E+41
200 2.1186E+90 1.2934E+88
300 1.3453E+137 5.4680E+134
400 1.0195E+184 3.1055E+181
500 8.5110E+230 2.0733E+228
1000 6.5068E+465 7.9187E+462
2000 1.0758E+936 6.5437E+932
3000 2.7387E+1406 1.1104E+1403
4000 8.3191E+1876 2.5295E+1873
5000 2.7839E+2347 6.7715E+2343
10000 2.2020E+4700 2.6779E+4696
(Possible precision error where 18 or more significant digits are shown)
The above results are the output of a computer program that would require a significant amount of explanation. I originally wrote the program in response to "Exercise 3." on page 395, Vol. 1, Knuth's "The Art of Computer Programming" (Second Edition). The derivation of the algorithm is spread over several pages in the "Enumeration of Trees" section. (If you like generating functions, have fun - otherwise, good luck.) Knuth's rating for the "Exercise" is "M40". Knuth's translation for this is: "Mathematically oriented" "Quite a difficult or lengthy problem, which is perhaps suitable for a term project in classroom situations." I will thus forgo trying to explain the algorithm although the computer code is surprisingly short. There are probably other sources that derive the algorithm. There will be other students that have to learn and understand the process. If you have the misfortune to find yourself in this position, you have my deepest sympathy.
Return to Durango Bill's Home Page
Web page generated via Sea Monkey's Composer HTML editor
within a Linux Cinnamon Mint 18 operating system.
(Goodbye Microsoft)
An interesting question arises. If you have any "N" number of vertices connected by "N-1" edges, how many structurally different trees are there of each type? We will present the results followed by a source that viewers can check if they want to know how to calculate the results.
Number of structurally different, rooted and non-rooted trees
Computer Program by Bill Butler
Number of Number of Number of
Vertices Rooted Trees Non-rooted trees
-----------------------------------------------------------------
1 1 1
2 1 1
3 2 1
4 4 2
5 9 3
6 20 6
7 48 11
8 115 23
9 286 47
10 719 106
11 1,842 235
12 4,766 551
13 12,486 1,301
14 32,973 3,159
15 87,811 7,741
16 235,381 19,320
17 634,847 48,629
18 1,721,159 123,867
19 4,688,676 317,955
20 12,826,228 823,065
21 35,221,832 2,144,505
22 97,055,181 5,623,756
23 268,282,855 14,828,074
24 743,724,984 39,299,897
25 2,067,174,645 104,636,890
26 5,759,636,510 279,793,450
27 16,083,734,329 751,065,460
28 45,007,066,269 2,023,443,032
29 126,186,554,308 5,469,566,585
30 354,426,847,597 14,830,871,802
31 997,171,512,998 40,330,829,030
32 2,809,934,352,700 109,972,410,221
33 7,929,819,784,355 300,628,862,480
34 22,409,533,673,568 823,779,631,721
35 63,411,730,258,053 2,262,366,343,746
36 179,655,930,440,464 6,226,306,037,178
37 509,588,049,810,620 17,169,677,490,714
38 1,447,023,384,581,029 47,436,313,524,262
39 4,113,254,119,923,150 131,290,543,779,126
40 11,703,780,079,612,453 363,990,257,783,343
41 33,333,125,878,283,632 1,010,748,076,717,151
42 95,020,085,893,954,917 2,810,986,483,493,475
43 271,097,737,169,671,824 7,828,986,221,515,605
44 774,088,023,431,472,074 21,835,027,912,963,086
45 2,212,039,245,722,726,118 60,978,390,985,918,906
46 6,325,843,306,177,425,928 170,508,699,155,987,862
47 1.8103E+19 477,355,090,753,926,459
48 5.1842E+19 1,337,946,100,045,842,280
49 1.4856E+20 3,754,194,185,716,399,992
50 4.2598E+20 1.0545E+19
100 5.1384E+43 6.3013E+41
200 2.1186E+90 1.2934E+88
300 1.3453E+137 5.4680E+134
400 1.0195E+184 3.1055E+181
500 8.5110E+230 2.0733E+228
1000 6.5068E+465 7.9187E+462
2000 1.0758E+936 6.5437E+932
3000 2.7387E+1406 1.1104E+1403
4000 8.3191E+1876 2.5295E+1873
5000 2.7839E+2347 6.7715E+2343
10000 2.2020E+4700 2.6779E+4696
(Possible precision error where 18 or more significant digits are shown)
The above results are the output of a computer program that would require a significant amount of explanation. I originally wrote the program in response to "Exercise 3." on page 395, Vol. 1, Knuth's "The Art of Computer Programming" (Second Edition). The derivation of the algorithm is spread over several pages in the "Enumeration of Trees" section. (If you like generating functions, have fun - otherwise, good luck.) Knuth's rating for the "Exercise" is "M40". Knuth's translation for this is: "Mathematically oriented" "Quite a difficult or lengthy problem, which is perhaps suitable for a term project in classroom situations." I will thus forgo trying to explain the algorithm although the computer code is surprisingly short. There are probably other sources that derive the algorithm. There will be other students that have to learn and understand the process. If you have the misfortune to find yourself in this position, you have my deepest sympathy.
Return to Durango Bill's Home Page
Web page generated via Sea Monkey's Composer HTML editor
within a Linux Cinnamon Mint 18 operating system.
(Goodbye Microsoft)