
Durango Bill's
Enumeration of Unlabeled Graphs
Enumeration of Structurally Different Unlabeled Graphs
An unlabeled graph
may have an arbitrary number of vertices with none, one, or
more edges connecting some or all of the vertices. A graph may
have several separate (not connected) subgraphs in the system.
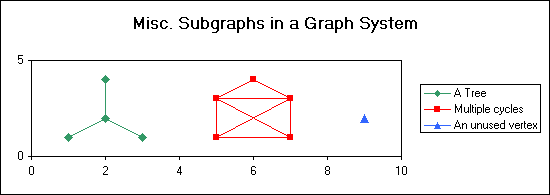
The chart above shows a graph containing 10 vertices and 11 edges. Four of the vertices are connected by 3 edges to form a tree. 5 more vertices are connected by 8 edges to form another subgraph that has multiple cycles. (You can travel along some (or all) the edges and return to your starting point.) Finally, vertices do not have to be connected to anything.
In any generalized graph system containing "V" vertices, there are potentially COMBIN(V, 2) edges that could be drawn. If we select any "E" of these for our graph, then there are COMBIN(COMBIN(V, 2), E) potential graph systems that could be drawn. A difficult problem in combinatorics is to calculate how many of these are structurally different.
The table below shows all combinations up to 13 vertices.
A typical row in the table translates as follows. If you have 2 edges and only 2 vertices, no graph is possible. If you have 2 edges and 3 vertices, 1 graph is possible. (Start at any vertex, draw the first edge to another vertex, and draw the 2nd edge to the remaining vertex. With 4 or more vertices, 2 structurally different graphs are possible. Each of the edges could connect a separate pair of vertices, or the edges could form a chain leaving one (or more) vertices unused.
At the end of the table I have included an outline on how to calculate these results. However, a full description of the process would require many pages explaining "Why" various calculations are being made.
Number
of <---------- Number of Vertices ----------->
Edges 2 3 4 5 6 7 8 9 10 11 12 13
-------------------------------------------------------------------------------------------------------
0 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1
2 0 1 2 2 2 2 2 2 2 2 2 2
3 0 1 3 4 5 5 5 5 5 5 5 5
4 0 0 2 6 9 10 11 11 11 11 11 11
5 0 0 1 6 15 21 24 25 26 26 26 26
6 0 0 1 6 21 41 56 63 66 67 68 68
7 0 0 0 4 24 65 115 148 165 172 175 176
8 0 0 0 2 24 97 221 345 428 467 485 492
9 0 0 0 1 21 131 402 771 1,103 1,305 1,405 1,446
10 0 0 0 1 15 148 663 1,637 2,769 3,664 4,191 4,435
11 0 0 0 0 9 148 980 3,252 6,759 10,250 12,763 14,140
12 0 0 0 0 5 131 1,312 5,995 15,772 28,259 39,243 46,415
13 0 0 0 0 2 97 1,557 10,120 34,663 75,415 119,890 154,658
14 0 0 0 0 1 65 1,646 15,615 71,318 192,788 359,307 517,121
15 0 0 0 0 1 41 1,557 21,933 136,433 467,807 1,043,774 1,711,908
16 0 0 0 0 0 21 1,312 27,987 241,577 1,069,890 2,911,086 5,546,619
17 0 0 0 0 0 10 980 32,403 395,166 2,295,898 7,739,601 17,422,984
18 0 0 0 0 0 5 663 34,040 596,191 4,609,179 19,515,361 52,664,857
19 0 0 0 0 0 2 402 32,403 828,728 8,640,134 46,505,609 152,339,952
20 0 0 0 0 0 1 221 27,987 1,061,159 15,108,047 104,504,341 420,048,805
21 0 0 0 0 0 1 115 21,933 1,251,389 24,630,887 221,147,351 1,101,083,128
22 0 0 0 0 0 0 56 15,615 1,358,852 37,433,760 440,393,606 2,739,261,020
23 0 0 0 0 0 0 24 10,120 1,358,852 53,037,356 825,075,506 6,461,056,816
24 0 0 0 0 0 0 11 5,995 1,251,389 70,065,437 1,454,265,734 14,441,470,390
25 0 0 0 0 0 0 5 3,252 1,061,159 86,318,670 2,411,961,516 30,583,652,956
26 0 0 0 0 0 0 2 1,637 828,728 99,187,806 3,765,262,970 61,372,294,334
27 0 0 0 0 0 0 1 771 596,191 106,321,628 5,534,255,092 116,724,411,757
28 0 0 0 0 0 0 1 345 395,166 106,321,628 7,661,345,277 210,474,287,115
29 0 0 0 0 0 0 0 148 241,577 99,187,806 9,992,340,187 359,954,668,522
30 0 0 0 0 0 0 0 63 136,433 86,318,670 12,281,841,209 584,089,835,857
31 0 0 0 0 0 0 0 25 71,318 70,065,437 14,229,503,560 899,632,282,299
32 0 0 0 0 0 0 0 11 34,663 53,037,356 15,542,350,436 1,315,729,343,451
33 0 0 0 0 0 0 0 5 15,772 37,433,760 16,006,173,014 1,827,823,498,798
34 0 0 0 0 0 0 0 2 6,759 24,630,887 15,542,350,436 2,412,694,353,115
35 0 0 0 0 0 0 0 1 2,769 15,108,047 14,229,503,560 3,026,821,673,656
36 0 0 0 0 0 0 0 1 1,103 8,640,134 12,281,841,209 3,609,810,088,490
37 0 0 0 0 0 0 0 0 428 4,609,179 9,992,340,187 4,093,273,437,761
38 0 0 0 0 0 0 0 0 165 2,295,898 7,661,345,277 4,413,678,080,790
39 0 0 0 0 0 0 0 0 66 1,069,890 5,534,255,092 4,525,920,859,198
40 0 0 0 0 0 0 0 0 26 467,807 3,765,262,970 4,413,678,080,790
41 0 0 0 0 0 0 0 0 11 192,788 2,411,961,516 4,093,273,437,761
42 0 0 0 0 0 0 0 0 5 75,415 1,454,265,734 3,609,810,088,490
43 0 0 0 0 0 0 0 0 2 28,259 825,075,506 3,026,821,673,656
44 0 0 0 0 0 0 0 0 1 10,250 440,393,606 2,412,694,353,115
45 0 0 0 0 0 0 0 0 1 3,664 221,147,351 1,827,823,498,798
46 0 0 0 0 0 0 0 0 0 1,305 104,504,341 1,315,729,343,451
47 0 0 0 0 0 0 0 0 0 467 46,505,609 899,632,282,299
48 0 0 0 0 0 0 0 0 0 172 19,515,361 584,089,835,857
49 0 0 0 0 0 0 0 0 0 67 7,739,601 359,954,668,522
50 0 0 0 0 0 0 0 0 0 26 2,911,086 210,474,287,115
51 0 0 0 0 0 0 0 0 0 11 1,043,774 116,724,411,757
52 0 0 0 0 0 0 0 0 0 5 359,307 61,372,294,334
53 0 0 0 0 0 0 0 0 0 2 119,890 30,583,652,956
54 0 0 0 0 0 0 0 0 0 1 39,243 14,441,470,390
55 0 0 0 0 0 0 0 0 0 1 12,763 6,461,056,816
56 0 0 0 0 0 0 0 0 0 0 4,191 2,739,261,020
57 0 0 0 0 0 0 0 0 0 0 1,405 1,101,083,128
58 0 0 0 0 0 0 0 0 0 0 485 420,048,805
59 0 0 0 0 0 0 0 0 0 0 175 152,339,952
60 0 0 0 0 0 0 0 0 0 0 68 52,664,857
61 0 0 0 0 0 0 0 0 0 0 26 17,422,984
62 0 0 0 0 0 0 0 0 0 0 11 5,546,619
63 0 0 0 0 0 0 0 0 0 0 5 1,711,908
64 0 0 0 0 0 0 0 0 0 0 2 517,121
65 0 0 0 0 0 0 0 0 0 0 1 154,658
66 0 0 0 0 0 0 0 0 0 0 1 46,415
67 0 0 0 0 0 0 0 0 0 0 0 14,140
68 0 0 0 0 0 0 0 0 0 0 0 4,435
69 0 0 0 0 0 0 0 0 0 0 0 1,446
70 0 0 0 0 0 0 0 0 0 0 0 492
71 0 0 0 0 0 0 0 0 0 0 0 176
72 0 0 0 0 0 0 0 0 0 0 0 68
73 0 0 0 0 0 0 0 0 0 0 0 26
74 0 0 0 0 0 0 0 0 0 0 0 11
75 0 0 0 0 0 0 0 0 0 0 0 5
76 0 0 0 0 0 0 0 0 0 0 0 2
77 0 0 0 0 0 0 0 0 0 0 0 1
78 0 0 0 0 0 0 0 0 0 0 0 1
-------------------------------------------------------------------------------------------------------
Totals 2 4 11 34 156 1,044 12,346 274,668 12,005,168 1,018,997,864 165,091,172,592 50,502,031,367,952
Results for all possible edges and for all possible vertices from 2 thru 70 can be seen here.
http://www.durangobill.com/MiscComb/UnlbGraph70.txt (2.1 MB file)
(Where 18 digits are shown, precision errors may exist, and are more likely where 19 digits are shown.)
The following table shows the number of possible graphs for larger numbers of vertices.
Number Number of Computer
of Vertices Possible Graphs Calculation Time
----------------------------------------------------------
10 12,005,168 0.000247 Sec.
20 6.4549E+38 0.004485 Sec.
30 3.3449E+98 0.137891 Sec.
40 7.7938E+186 2.19931 Sec.
50 1.8996E+304 26.7119 Sec.
60 7.9968E+450 207.492 Sec.
70 8.1103E+626 1,437.1 Sec.
80 2.5122E+832 8,431.77 Sec.
90 2.8392E+1067 43,855.6 Sec.
100 1.3442E+1332 205,642 Sec.
(Calculations for another 10 (+/-) more rows are possible, but would be excessively time consuming.)
A listing of the number of all possible graphs for each possible edge for 80 vertices can be seen here:
http://www.durangobill.com/MiscComb/UnlbGraph80.txt
Note: The total number of graphs given here cross checks with the exact number given at https://oeis.org/A000088/b000088.txt , but the author of this web page also lists the subtotals for each number of edges in the graphs.
A listing of the number of all possible graphs for each possible edge for 90 vertices can be seen here:
http://www.durangobill.com/MiscComb/UnlbGraph90.txt
A listing of the number of all possible graphs for each possible edge for 100 vertices can be seen here:
http://www.durangobill.com/MiscComb/UnlbGraph100.txt
(Up to 4,950 possible edges)
Calculations are a "little" involved. First, for each column (Number of Vertices) you have to generate the "Cycle Index Formula for the Symmetric Groups". The Cycle Index Formula for 5 vertices is shown below. (The web editor leaves a "little" to be desired for subscripts and superscripts, but I hope you get the idea.)
1 5 3 2 2 ("1 over" & Superscripts)
Z(S ) = --(s + 10s s + 20s s + 15s s + 30s s + 20s s + 24s ) (Main line)
5 5! 1 1 2 1 3 1 2 1 4 2 3 5 (FACT(5) & Subscripts)
(Note: In this and the following equation, if no superscript (power) is shown, it is an implied "1".) The first term is "1" divided by FACT(Nbr. of Vertices). The terms inside the parenthesis are derived from the way 5 objects can be partitioned. (Five 1's, three 1's and one 2, two 1's and one 3, one 1 and two 2's, one 1 and one 4, one 2 and one 3, one 5.) The coefficient for each term inside the parenthesis is calculated by starting with 5! = 120. Then for each "s" in each term, first divide by FACT(Superscript). Then divide again by Subscript^Superscript.
Next we have to convert the "Cycle Index Formula for the Symmetric Groups" (above) to the "Cycle Index Formula for the Pair Groups". For our 5-vertex equation this becomes:
(2) 1 10 4 3 3 2 4 2 2
Z(S ) = --(s + 10s s + 20s s + 15s s + 30s s + 20s s s + 24s )
5 5! 1 1 2 1 3 1 2 2 4 1 3 6 5
The conversion for each of the terms inside the parenthesis (in our 5 vertex example there are 7 terms) is calculated as follows: For each "s" in each term let "k" equal the old subscript and "JsubK" equal the old superscript. Then if "k" is odd, the new subscript simply copies "k". The new superscript becomes: (JsubK)*[((k)(JsubK)-1)/2]. (Note: If the superscript goes to "0", the "s" disappears.)
If "k" is even, then the single "s" expands into 2 "s" components. For the first of these, the superscript remains the same while the subscript is divided by 2. For the second "s" the subscript remains the same while the new superscript becomes: (JsubK)*[((k)(JsubK)-2)/2)]. (Note: Again, if the superscript goes to "0", the "s" disappears.)
Finally, for each of the (old) terms that have two or more "s" components, then for each possible pair of s's, we generate a new "s" where the new subscript is the least common multiple of the subscripts of the two s's in the pair, and the superscript equals: the product of the two superscripts and multiplied again by the greatest common divisor of the two superscripts.
As an example of how these calculations work, let's work with the second term in the first equation. The first "s" has an odd subscript. Thus, the old subscript "1" stays at "1". The new superscript becomes: 3[((1)(3)-1)/2] = 3.
The second "s" is even, thus we will have two resulting "s" terms. The first of these keeps the old superscript of "1" while the subscript gets cut in half to "1". The second "s" term will keep the old subscript of "2" and the new superscript becomes: 1[(2)(1)-2)/2] = 0. (This "s" will thus disappear.)
Finally, there are 2 "s" terms in the first equation. Thus will have to apply the pair rule once. The subscript will be:
LCM(1, 2) = 2. The superscript for the new "s" will be: (3)(1)[GCD(3, 1)] = 3.
Combining these three operations yields:
3 1 0 3 4 3
Converted term = (10)(s )(s )(s )(s ) = (10)(s )(s )
1 1 2 2 1 2
When we combine and simplify these new terms we get the "Cycle Index Formula for the Pair Groups". If all you want to know is the total number of structurally different graphs (without a breakdown by specific number of edges), you can use the "Pair" equation.
For example, if your graph is confined to 2 "colors" (either an edge exists or it doesn't), simply substitute "2" for each "s" in the "Pair" equation. (This will give you the grand total shown at the bottom of the table.) If you want 3 "colors" (e. g. No edge, green edge, or black edge), substitute a "3" instead.
For the 5 vertex "Pair" equation, if we substitute "2" for "s" it becomes:
Total combinations = 1/5! [2^10 + 10(2^4)(2^3) + 20(2)(2^3) + 15(2^2)(2^4) + 30(2)(2^2) + 20(2)(2)(2) + 24(2^2)] = 34
If you want the complete Edge/Vertex table, another step is required. To get the results shown in the table: substitute "1 + Y" for each "s" and then use the subscripts and superscripts to perform the following polynomial multiplication: ((1 + Y^(Subscript))^Superscript). Then add the polynomials for each term. For example: The second term in the "Pair" formula becomes: 10[((1 + Y^1)^4) + ((1 + Y^2)^3)].
After you have combined all the terms for the Number of Vertices = 5 formula you will get:
(1/5!) * [ 120 + 120Y + 240Y^2 + 480Y^3 + 720Y^4 + 720Y^5 + 720Y^6 + 480Y^7 + 240Y^8 + 120Y^9 + 120Y^10]
which reduces to the values in the table.
("Y" = the number of colors available. If your graph has just "black" edges, you have "1" color. Thus substitute "1" for Y. Each term will give the number of unlabeled graphs for the corresponding number of edges. If edges (if present) can be either red or green (2 colors), then substitute "2" for Y. Etc.)
Return to Durango Bill's Home Page
Web page generated via Sea Monkey's Composer HTML editor
within a Linux Cinnamon Mint 18 operating system.
(Goodbye Microsoft)
The chart above shows a graph containing 10 vertices and 11 edges. Four of the vertices are connected by 3 edges to form a tree. 5 more vertices are connected by 8 edges to form another subgraph that has multiple cycles. (You can travel along some (or all) the edges and return to your starting point.) Finally, vertices do not have to be connected to anything.
In any generalized graph system containing "V" vertices, there are potentially COMBIN(V, 2) edges that could be drawn. If we select any "E" of these for our graph, then there are COMBIN(COMBIN(V, 2), E) potential graph systems that could be drawn. A difficult problem in combinatorics is to calculate how many of these are structurally different.
The table below shows all combinations up to 13 vertices.
A typical row in the table translates as follows. If you have 2 edges and only 2 vertices, no graph is possible. If you have 2 edges and 3 vertices, 1 graph is possible. (Start at any vertex, draw the first edge to another vertex, and draw the 2nd edge to the remaining vertex. With 4 or more vertices, 2 structurally different graphs are possible. Each of the edges could connect a separate pair of vertices, or the edges could form a chain leaving one (or more) vertices unused.
At the end of the table I have included an outline on how to calculate these results. However, a full description of the process would require many pages explaining "Why" various calculations are being made.
Number of structurally
different unlabeled graphs for "V" vertices and "E" edges
Computer Program by Bill Butler
Computer Program by Bill Butler
Number
of <---------- Number of Vertices ----------->
Edges 2 3 4 5 6 7 8 9 10 11 12 13
-------------------------------------------------------------------------------------------------------
0 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1
2 0 1 2 2 2 2 2 2 2 2 2 2
3 0 1 3 4 5 5 5 5 5 5 5 5
4 0 0 2 6 9 10 11 11 11 11 11 11
5 0 0 1 6 15 21 24 25 26 26 26 26
6 0 0 1 6 21 41 56 63 66 67 68 68
7 0 0 0 4 24 65 115 148 165 172 175 176
8 0 0 0 2 24 97 221 345 428 467 485 492
9 0 0 0 1 21 131 402 771 1,103 1,305 1,405 1,446
10 0 0 0 1 15 148 663 1,637 2,769 3,664 4,191 4,435
11 0 0 0 0 9 148 980 3,252 6,759 10,250 12,763 14,140
12 0 0 0 0 5 131 1,312 5,995 15,772 28,259 39,243 46,415
13 0 0 0 0 2 97 1,557 10,120 34,663 75,415 119,890 154,658
14 0 0 0 0 1 65 1,646 15,615 71,318 192,788 359,307 517,121
15 0 0 0 0 1 41 1,557 21,933 136,433 467,807 1,043,774 1,711,908
16 0 0 0 0 0 21 1,312 27,987 241,577 1,069,890 2,911,086 5,546,619
17 0 0 0 0 0 10 980 32,403 395,166 2,295,898 7,739,601 17,422,984
18 0 0 0 0 0 5 663 34,040 596,191 4,609,179 19,515,361 52,664,857
19 0 0 0 0 0 2 402 32,403 828,728 8,640,134 46,505,609 152,339,952
20 0 0 0 0 0 1 221 27,987 1,061,159 15,108,047 104,504,341 420,048,805
21 0 0 0 0 0 1 115 21,933 1,251,389 24,630,887 221,147,351 1,101,083,128
22 0 0 0 0 0 0 56 15,615 1,358,852 37,433,760 440,393,606 2,739,261,020
23 0 0 0 0 0 0 24 10,120 1,358,852 53,037,356 825,075,506 6,461,056,816
24 0 0 0 0 0 0 11 5,995 1,251,389 70,065,437 1,454,265,734 14,441,470,390
25 0 0 0 0 0 0 5 3,252 1,061,159 86,318,670 2,411,961,516 30,583,652,956
26 0 0 0 0 0 0 2 1,637 828,728 99,187,806 3,765,262,970 61,372,294,334
27 0 0 0 0 0 0 1 771 596,191 106,321,628 5,534,255,092 116,724,411,757
28 0 0 0 0 0 0 1 345 395,166 106,321,628 7,661,345,277 210,474,287,115
29 0 0 0 0 0 0 0 148 241,577 99,187,806 9,992,340,187 359,954,668,522
30 0 0 0 0 0 0 0 63 136,433 86,318,670 12,281,841,209 584,089,835,857
31 0 0 0 0 0 0 0 25 71,318 70,065,437 14,229,503,560 899,632,282,299
32 0 0 0 0 0 0 0 11 34,663 53,037,356 15,542,350,436 1,315,729,343,451
33 0 0 0 0 0 0 0 5 15,772 37,433,760 16,006,173,014 1,827,823,498,798
34 0 0 0 0 0 0 0 2 6,759 24,630,887 15,542,350,436 2,412,694,353,115
35 0 0 0 0 0 0 0 1 2,769 15,108,047 14,229,503,560 3,026,821,673,656
36 0 0 0 0 0 0 0 1 1,103 8,640,134 12,281,841,209 3,609,810,088,490
37 0 0 0 0 0 0 0 0 428 4,609,179 9,992,340,187 4,093,273,437,761
38 0 0 0 0 0 0 0 0 165 2,295,898 7,661,345,277 4,413,678,080,790
39 0 0 0 0 0 0 0 0 66 1,069,890 5,534,255,092 4,525,920,859,198
40 0 0 0 0 0 0 0 0 26 467,807 3,765,262,970 4,413,678,080,790
41 0 0 0 0 0 0 0 0 11 192,788 2,411,961,516 4,093,273,437,761
42 0 0 0 0 0 0 0 0 5 75,415 1,454,265,734 3,609,810,088,490
43 0 0 0 0 0 0 0 0 2 28,259 825,075,506 3,026,821,673,656
44 0 0 0 0 0 0 0 0 1 10,250 440,393,606 2,412,694,353,115
45 0 0 0 0 0 0 0 0 1 3,664 221,147,351 1,827,823,498,798
46 0 0 0 0 0 0 0 0 0 1,305 104,504,341 1,315,729,343,451
47 0 0 0 0 0 0 0 0 0 467 46,505,609 899,632,282,299
48 0 0 0 0 0 0 0 0 0 172 19,515,361 584,089,835,857
49 0 0 0 0 0 0 0 0 0 67 7,739,601 359,954,668,522
50 0 0 0 0 0 0 0 0 0 26 2,911,086 210,474,287,115
51 0 0 0 0 0 0 0 0 0 11 1,043,774 116,724,411,757
52 0 0 0 0 0 0 0 0 0 5 359,307 61,372,294,334
53 0 0 0 0 0 0 0 0 0 2 119,890 30,583,652,956
54 0 0 0 0 0 0 0 0 0 1 39,243 14,441,470,390
55 0 0 0 0 0 0 0 0 0 1 12,763 6,461,056,816
56 0 0 0 0 0 0 0 0 0 0 4,191 2,739,261,020
57 0 0 0 0 0 0 0 0 0 0 1,405 1,101,083,128
58 0 0 0 0 0 0 0 0 0 0 485 420,048,805
59 0 0 0 0 0 0 0 0 0 0 175 152,339,952
60 0 0 0 0 0 0 0 0 0 0 68 52,664,857
61 0 0 0 0 0 0 0 0 0 0 26 17,422,984
62 0 0 0 0 0 0 0 0 0 0 11 5,546,619
63 0 0 0 0 0 0 0 0 0 0 5 1,711,908
64 0 0 0 0 0 0 0 0 0 0 2 517,121
65 0 0 0 0 0 0 0 0 0 0 1 154,658
66 0 0 0 0 0 0 0 0 0 0 1 46,415
67 0 0 0 0 0 0 0 0 0 0 0 14,140
68 0 0 0 0 0 0 0 0 0 0 0 4,435
69 0 0 0 0 0 0 0 0 0 0 0 1,446
70 0 0 0 0 0 0 0 0 0 0 0 492
71 0 0 0 0 0 0 0 0 0 0 0 176
72 0 0 0 0 0 0 0 0 0 0 0 68
73 0 0 0 0 0 0 0 0 0 0 0 26
74 0 0 0 0 0 0 0 0 0 0 0 11
75 0 0 0 0 0 0 0 0 0 0 0 5
76 0 0 0 0 0 0 0 0 0 0 0 2
77 0 0 0 0 0 0 0 0 0 0 0 1
78 0 0 0 0 0 0 0 0 0 0 0 1
-------------------------------------------------------------------------------------------------------
Totals 2 4 11 34 156 1,044 12,346 274,668 12,005,168 1,018,997,864 165,091,172,592 50,502,031,367,952
Results for all possible edges and for all possible vertices from 2 thru 70 can be seen here.
http://www.durangobill.com/MiscComb/UnlbGraph70.txt (2.1 MB file)
(Where 18 digits are shown, precision errors may exist, and are more likely where 19 digits are shown.)
The following table shows the number of possible graphs for larger numbers of vertices.
Number Number of Computer
of Vertices Possible Graphs Calculation Time
----------------------------------------------------------
10 12,005,168 0.000247 Sec.
20 6.4549E+38 0.004485 Sec.
30 3.3449E+98 0.137891 Sec.
40 7.7938E+186 2.19931 Sec.
50 1.8996E+304 26.7119 Sec.
60 7.9968E+450 207.492 Sec.
70 8.1103E+626 1,437.1 Sec.
80 2.5122E+832 8,431.77 Sec.
90 2.8392E+1067 43,855.6 Sec.
100 1.3442E+1332 205,642 Sec.
(Calculations for another 10 (+/-) more rows are possible, but would be excessively time consuming.)
A listing of the number of all possible graphs for each possible edge for 80 vertices can be seen here:
http://www.durangobill.com/MiscComb/UnlbGraph80.txt
Note: The total number of graphs given here cross checks with the exact number given at https://oeis.org/A000088/b000088.txt , but the author of this web page also lists the subtotals for each number of edges in the graphs.
A listing of the number of all possible graphs for each possible edge for 90 vertices can be seen here:
http://www.durangobill.com/MiscComb/UnlbGraph90.txt
A listing of the number of all possible graphs for each possible edge for 100 vertices can be seen here:
http://www.durangobill.com/MiscComb/UnlbGraph100.txt
(Up to 4,950 possible edges)
Calculations are a "little" involved. First, for each column (Number of Vertices) you have to generate the "Cycle Index Formula for the Symmetric Groups". The Cycle Index Formula for 5 vertices is shown below. (The web editor leaves a "little" to be desired for subscripts and superscripts, but I hope you get the idea.)
1 5 3 2 2 ("1 over" & Superscripts)
Z(S ) = --(s + 10s s + 20s s + 15s s + 30s s + 20s s + 24s ) (Main line)
5 5! 1 1 2 1 3 1 2 1 4 2 3 5 (FACT(5) & Subscripts)
(Note: In this and the following equation, if no superscript (power) is shown, it is an implied "1".) The first term is "1" divided by FACT(Nbr. of Vertices). The terms inside the parenthesis are derived from the way 5 objects can be partitioned. (Five 1's, three 1's and one 2, two 1's and one 3, one 1 and two 2's, one 1 and one 4, one 2 and one 3, one 5.) The coefficient for each term inside the parenthesis is calculated by starting with 5! = 120. Then for each "s" in each term, first divide by FACT(Superscript). Then divide again by Subscript^Superscript.
Next we have to convert the "Cycle Index Formula for the Symmetric Groups" (above) to the "Cycle Index Formula for the Pair Groups". For our 5-vertex equation this becomes:
(2) 1 10 4 3 3 2 4 2 2
Z(S ) = --(s + 10s s + 20s s + 15s s + 30s s + 20s s s + 24s )
5 5! 1 1 2 1 3 1 2 2 4 1 3 6 5
The conversion for each of the terms inside the parenthesis (in our 5 vertex example there are 7 terms) is calculated as follows: For each "s" in each term let "k" equal the old subscript and "JsubK" equal the old superscript. Then if "k" is odd, the new subscript simply copies "k". The new superscript becomes: (JsubK)*[((k)(JsubK)-1)/2]. (Note: If the superscript goes to "0", the "s" disappears.)
If "k" is even, then the single "s" expands into 2 "s" components. For the first of these, the superscript remains the same while the subscript is divided by 2. For the second "s" the subscript remains the same while the new superscript becomes: (JsubK)*[((k)(JsubK)-2)/2)]. (Note: Again, if the superscript goes to "0", the "s" disappears.)
Finally, for each of the (old) terms that have two or more "s" components, then for each possible pair of s's, we generate a new "s" where the new subscript is the least common multiple of the subscripts of the two s's in the pair, and the superscript equals: the product of the two superscripts and multiplied again by the greatest common divisor of the two superscripts.
As an example of how these calculations work, let's work with the second term in the first equation. The first "s" has an odd subscript. Thus, the old subscript "1" stays at "1". The new superscript becomes: 3[((1)(3)-1)/2] = 3.
The second "s" is even, thus we will have two resulting "s" terms. The first of these keeps the old superscript of "1" while the subscript gets cut in half to "1". The second "s" term will keep the old subscript of "2" and the new superscript becomes: 1[(2)(1)-2)/2] = 0. (This "s" will thus disappear.)
Finally, there are 2 "s" terms in the first equation. Thus will have to apply the pair rule once. The subscript will be:
LCM(1, 2) = 2. The superscript for the new "s" will be: (3)(1)[GCD(3, 1)] = 3.
Combining these three operations yields:
3 1 0 3 4 3
Converted term = (10)(s )(s )(s )(s ) = (10)(s )(s )
1 1 2 2 1 2
When we combine and simplify these new terms we get the "Cycle Index Formula for the Pair Groups". If all you want to know is the total number of structurally different graphs (without a breakdown by specific number of edges), you can use the "Pair" equation.
For example, if your graph is confined to 2 "colors" (either an edge exists or it doesn't), simply substitute "2" for each "s" in the "Pair" equation. (This will give you the grand total shown at the bottom of the table.) If you want 3 "colors" (e. g. No edge, green edge, or black edge), substitute a "3" instead.
For the 5 vertex "Pair" equation, if we substitute "2" for "s" it becomes:
Total combinations = 1/5! [2^10 + 10(2^4)(2^3) + 20(2)(2^3) + 15(2^2)(2^4) + 30(2)(2^2) + 20(2)(2)(2) + 24(2^2)] = 34
If you want the complete Edge/Vertex table, another step is required. To get the results shown in the table: substitute "1 + Y" for each "s" and then use the subscripts and superscripts to perform the following polynomial multiplication: ((1 + Y^(Subscript))^Superscript). Then add the polynomials for each term. For example: The second term in the "Pair" formula becomes: 10[((1 + Y^1)^4) + ((1 + Y^2)^3)].
After you have combined all the terms for the Number of Vertices = 5 formula you will get:
(1/5!) * [ 120 + 120Y + 240Y^2 + 480Y^3 + 720Y^4 + 720Y^5 + 720Y^6 + 480Y^7 + 240Y^8 + 120Y^9 + 120Y^10]
which reduces to the values in the table.
("Y" = the number of colors available. If your graph has just "black" edges, you have "1" color. Thus substitute "1" for Y. Each term will give the number of unlabeled graphs for the corresponding number of edges. If edges (if present) can be either red or green (2 colors), then substitute "2" for Y. Etc.)
Return to Durango Bill's Home Page
Web page generated via Sea Monkey's Composer HTML editor
within a Linux Cinnamon Mint 18 operating system.
(Goodbye Microsoft)