Suppose you have (or are planning to construct) cell phone towers “randomly” scattered over the countryside. Again, suppose you wish to draw a map so that customers will know what is the nearest cell phone tower to their location. Alternately, suppose you are the telephone company and would like to estimate the volume of electronic traffic that will go through each tower based on the population within each zone. What would such a map look like?



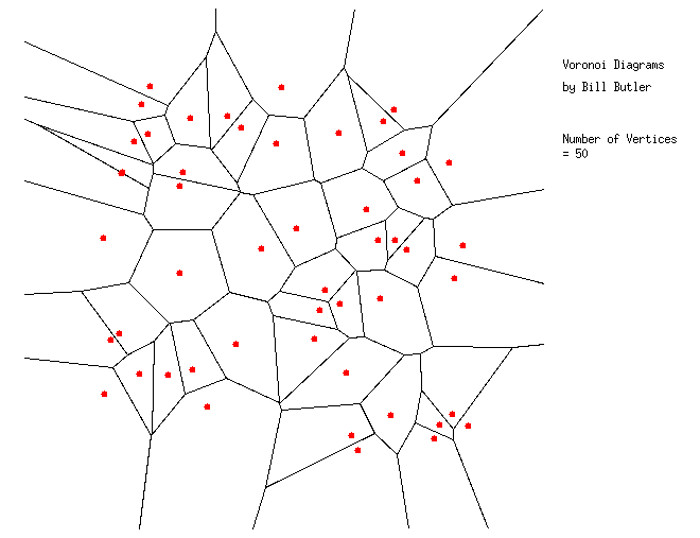
   The solution to this problem is a Voronoi Diagram. In the above diagram, the white area within the surrounding black lines shows all locations that are closer to the local red dot than they are to any other red dot.

   The black lines are perpendicular bisectors of (not drawn) lines joining two neighborly red dots. Every point on a black line is equally distant from the two relevant red dots. The black lines that form this diagram are usually called Voronoi polygons.

   Of note, there is a black line that appears to go through a red dot in the upper left quadrant of the diagram. What happened is that two red dots were very close to each other so that they appear as one dot at the displayed screen resolution. The black line that appears to go through the red dot is actually a perpendicular bisector of the line connecting the two very close red dots.

   The black lines form junctions at triple points. These junctions are actually equidistant from all three relevant red dots. The computer program that solves the Voronoi problem calculates the x/y coordinates of these triple points and uses adjacent triple points to define and draw the black lines.

   For mathematically oriented readers who would like to know how the coordinates of these triple points are found, think back to your old “algebra days”. Do you remember anything about finding the intersection point of two non-parallel lines? (And the lines are the perpendicular bisectors of two “neighborly” red dots – and we are given the locations (x/y coordinates) of the red dots as part of the problem.)


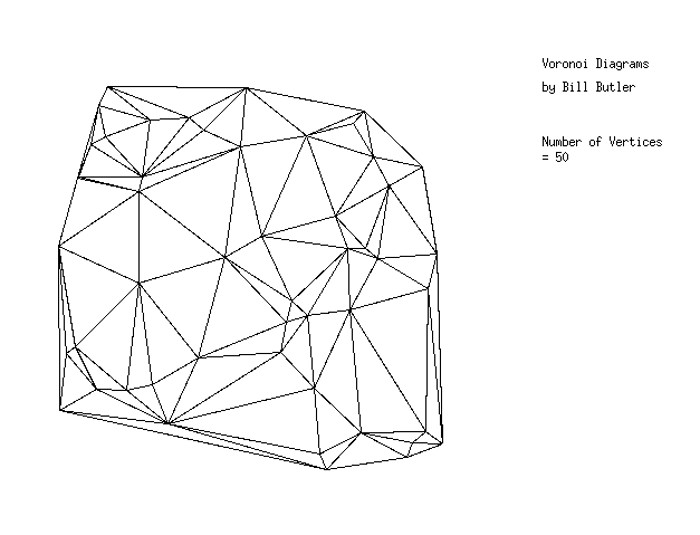
   Earlier, we said the the black lines in the Voronoi diagram were the perpendicular bisectors of the (not drawn) lines connecting the “neighborly” red dots. If we instead draw these lines that connect the red dots, we get a Voronoi Triangulation. (Also called Delaunay Triangulation)

   A Voronoi Triangulation is an efficient (but not necessarily optimal) subdivision of the area involved into triangles. These triangles are useful for computer generated images (and video/movies) since colors can be assigned to each triangle to generate an image. When the colors at the triangle boundaries are blurred, the result can be a very realistic picture. In turn a sequence of individual pictures can be run in sequence to form a video. The end result can be your typical shoot-em-up, space-invader game.


   A large number of vertexes can be used to form another version of “computer art”. The diagram above used 5,000 random red dots/vertexes spread over a circle along with the calculated resultant Voronoi Diagram. The result resembles a sun burst.



For another example using graphics programming, please see the author's web page at:
http://www.durangobill.com/TravelingSalesman/TravelingSalesman.html
The Traveling Salesman Problem



Web page generated via Sea Monkey's Composer HTML editor
within  a Linux Cinnamon Mint 18 operating system.
(Goodbye Microsoft)

Return to Durango Bill's home page